
(08年芜湖一中理)若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其定义域上的任意实数
对其定义域上的任意实数![]() 分别满足:
分别满足:![]() 和
和![]() ,则称直线
,则称直线![]()
![]() 为
为![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的极值;
的极值;
(2) 函数![]() 和
和![]() 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
解:(1) ![]()
![]() ,
, ![]() .
.
当![]() 时,
时,![]() .
.
![]() 当
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递减;
递减;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递增;
递增;
∴当![]() 时,
时,![]() 取极小值,其极小值为
取极小值,其极小值为![]() .…………6分
.…………6分
(2)解法一:由(1)可知函数![]() 和
和![]() 的图象在
的图象在![]() 处有公共点,
处有公共点,
因此若存在![]() 和
和![]() 的隔离直线,则该直线过这个公共点.
的隔离直线,则该直线过这个公共点.
设隔离直线的斜率为![]() ,则直线方程为
,则直线方程为![]() ,即
,即![]() .
.
由![]() ,可得
,可得![]() 当
当![]() 时恒成立
时恒成立
![]() ,
, ![]() 由
由![]() ,得
,得![]() .
.
下面证明![]() 当
当![]() 时恒成立.令
时恒成立.令![]()
![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() .
.
![]() 当
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递增;
递增;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递减;
递减;
∴当![]() 时,
时,![]() 取极大值,其极大值为
取极大值,其极大值为![]() .
.
从而![]() ,即
,即![]() 恒成立.
恒成立.
∴函数![]() 和
和![]() 存在唯一的隔离直线
存在唯一的隔离直线![]() .…………………12分
.…………………12分
解法二: 由(1)可知当![]() 时,
时,![]() (当且当
(当且当![]() 时取等号) .
时取等号) .
若存在![]() 和
和![]() 的隔离直线,则存在实常数
的隔离直线,则存在实常数![]() 和
和![]() ,使得
,使得![]() 和
和![]() 恒成立,
恒成立,
令![]() ,则
,则![]() 且
且![]()


科目:高中数学 来源: 题型:
(08年芜湖一中理) 已知数列{an},Sn是其前n项和,且![]() ,(1)求数列{an}的通项公式;(2)设
,(1)求数列{an}的通项公式;(2)设![]() 是数列{bn}的前n项和,求使得
是数列{bn}的前n项和,求使得![]() 对所有
对所有![]() 都成立的最小正整数m.
都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
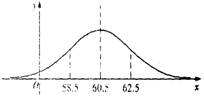
(08年芜湖一中理)某单位1 000名青年职员的体重x ( kg )服从正态分布N (![]() , 22 ),且正态分布的密度曲线如图所示,若58.5 ~ 62.5 kg体重属于正常情况,则这1 000名青年职员中体重属于正常情况的人数约是(其中
, 22 ),且正态分布的密度曲线如图所示,若58.5 ~ 62.5 kg体重属于正常情况,则这1 000名青年职员中体重属于正常情况的人数约是(其中![]() (1)≈0.841)( )
(1)≈0.841)( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com