
【题目】已知函数![]() ,(
,(![]() 为自然对数的底数)
为自然对数的底数)
(I)若![]() 在
在![]() 上单调递减,求
上单调递减,求![]() 的最大值;
的最大值;
(Ⅱ)当![]() 时,证明:
时,证明:![]() .
.
科目:高中数学 来源: 题型:
【题目】某书店销售刚刚上市的某高二数学单元测试卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
单价x/元 | 18 | 19 | 20 | 21 | 22 |
销量y/册 | 61 | 56 | 50 | 48 | 45 |
(1)求试销![]() 天的销量的方差和
天的销量的方差和![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
附: 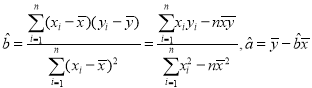 .
.
(2)预计以后的销售中,销量与单价服从上题中的回归直线方程,已知每册单元测试卷的成本是10元,为了获得最大利润,该单元测试卷的单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当![]() ,求函数
,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作.其中的一道题“今有木,方三尺,高三尺,欲方五寸作枕一枚.问:得几何?”意思是:“有一块棱长为3尺的正方体方木,要把它作成边长为5寸的正方体枕头,可作多少个?”现有这样的一个正方体木料,其外周已涂上油漆,则从切割后的正方体枕头中任取一块,恰有一面涂上油漆的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校命制了一套调查问卷(试卷满分均为100分),并对整个学校的学生进行了测试,先从这些学生的成绩中随机抽取了50名学生的成绩,按照![]() 分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分)
分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分)
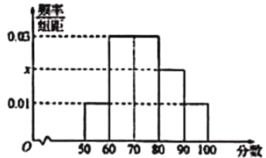
(1)求频率分布直方图中的![]() 的值,并估计50名学生的成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表)
的值,并估计50名学生的成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表)
(2)用样本估计总体,若该校共有2000名学生,试估计该校这次成绩不低于70分的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com