练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】执行如图所示的程序框图，输出的S值为（　　）

    A.2
    B.
    C.
    D.

    【答案】C
    【解析】解：当k=0时，满足进行循环的条件，执行完循环体后，k=1，S=2，
    当k=1时，满足进行循环的条件，执行完循环体后，k=2，S= ，
    当k=2时，满足进行循环的条件，执行完循环体后，k=3，S= ，
    当k=3时，不满足进行循环的条件，
    故输出结果为： ，
    故选：C．
    【考点精析】解答此题的关键在于理解算法的循环结构的相关知识，掌握在一些算法中，经常会出现从某处开始，按照一定条件，反复执行某一处理步骤的情况，这就是循环结构，循环结构可细分为两类：当型循环结构和直到型循环结构，以及对程序框图的理解，了解程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C所对的边分别为a，b，c．已知a＞b，a=5，c=6，sinB= ．
    （Ⅰ）求b和sinA的值；
    （Ⅱ）求sin（2A+ ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数f（x）=x2+ax+b在区间[0，1]上的最大值是M，最小值是m，则M﹣m（ ）
    A.与a有关，且与b有关
    B.与a有关，但与b无关
    C.与a无关，且与b无关
    D.与a无关，但与b有关

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列的公差不为零，，且成等比数列．

    (1)求的通项公式；

    (2)求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体ABCD中，下面结论错误的是( )

    A. BD∥平面C B. AC1⊥BD

    C. AC1⊥平面C D. 向量与的夹角为60°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，PA=PD= ，AB=4．（14分）
    （1）求证：M为PB的中点；
    （2）求二面角B﹣PD﹣A的大小；
    （3）求直线MC与平面BDP所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,如图,以C为原点,分别以CA,CB,CC1为x,y,z轴建立空间直角坐标系.

    (1)求平面A1B1C的法向量;

    (2)求直线AC与平面A1B1C夹角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在底面为平行四边形的四棱锥O-ABCD中,BC⊥平面OAB,E为OB中点,OA=AD=2AB=2,OB=.

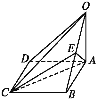
    (1)求证:平面OAD⊥平面ABCD;

    (2)求二面角B-AC-E的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知坐标平面内三点P(3，-1),M(6，2),N,直线过点P.若直线与线段MN相交，则直线的倾斜角的取值范围（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案