
【题目】已知 ![]() ,且
,且 ![]() .
.
(1)化简f(a);
(2)若 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:∵ ![]() ,
,
∴sinα∈(0,1),cosα∈(0,1),
∴ ![]() =cosα
=cosα ![]() +sinα
+sinα ![]() =1﹣sinα+1﹣cosα=2﹣sinα﹣cosα.
=1﹣sinα+1﹣cosα=2﹣sinα﹣cosα.
(2)解:∵ ![]() =2﹣sinα﹣cosα,
=2﹣sinα﹣cosα,
∴sinα+cosα= ![]() ,
,
∴两边平方可得:1+2sinαcosα= ![]() ,解得:sinαcosα=
,解得:sinαcosα= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= 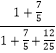 =
= ![]() .
.
【解析】(1)由已知可得sinα∈(0,1),cosα∈(0,1),利用同角三角函数基本关系式化简化简得解.(2)由已知可求sinα+cosα= ![]() ,两边平方可得sinαcosα=
,两边平方可得sinαcosα= ![]() ,将所求通分后化简即可计算得解.
,将所求通分后化简即可计算得解.
【考点精析】关于本题考查的同角三角函数基本关系的运用,需要了解同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为 . 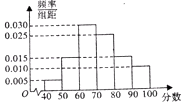
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:2ax+y﹣1=0,l2:ax+(a﹣1)y+1=0,
(1)若l1⊥l2 , 求实数a的值;
(2)若l1∥l2时,求直线l1与l2之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系中, ![]() 为极点,半径为2的圆
为极点,半径为2的圆![]() 的圆心坐标为
的圆心坐标为![]() .
.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设直角坐标系的原点与极点![]() 重合,
重合, ![]() 轴非负关轴与极轴重合,直线
轴非负关轴与极轴重合,直线![]() 的参数方程为
的参数方程为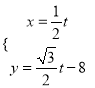 (
(![]() 为参数),由直线
为参数),由直线![]() 上的点向圆
上的点向圆![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,若
,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)在(1)的条件下,设![]() 为整数,且对于任意正整数
为整数,且对于任意正整数![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1= ![]() ,an+1﹣an+anan+1=0(n∈N*).
,an+1﹣an+anan+1=0(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:a1+a1a2+a1a2a3+…+a1a2…an<1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com