
【题目】如图,已知四棱锥![]() 的底面是边长为
的底面是边长为![]() 的菱形,
的菱形,![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,点
,点![]() 在平面
在平面![]() 的射影为
的射影为![]() ,
,![]() 为棱
为棱![]() 上一点,
上一点,
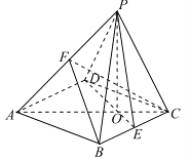
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,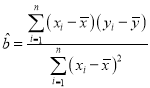
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》卷第五《商功》中,有“贾令刍童,上广一尺,袤二尺,下广三尺,袤四尺,高一尺。”,意思是:“假设一个刍童,上底面宽1尺,长2尺;下底面宽3尺,长4尺,高1尺(如图)。”(注:刍童为上下底面为相互平行的不相似长方形,两底面的中心连线与底面垂直的几何体),若该几何体所有顶点在一球体的表面上,则该球体的表面积为( )
A. ![]() 平方尺 B.
平方尺 B. ![]() 平方尺 C.
平方尺 C. ![]() 平方尺 D.
平方尺 D. ![]() 平方尺
平方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导数f'(x),x∈R,有f(-x)+f(x)=x2,在(0,+∞)上,f'(x)<x,若f(6-m)-f(m)-18+6m≥0,则实数m的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() R.
R.
(Ⅰ)求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若对任意的实数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,若对任意的实数
,若对任意的实数![]() ,关于
,关于![]() 的方程
的方程![]() 有且只有两个不同的实根,求实数
有且只有两个不同的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com