Question

【题目】一个大型喷水池的中央有一个强力喷水柱，为了测量喷水柱喷水的高度，某人在喷水柱正西方向的点A测的水柱顶端的仰角为45°，沿点A向北偏东30°前进100m到达点B．在B点测得水柱顶端的仰角为30°，则水柱的高度是 ．

Answer 1

【答案】50m
【解析】解：如图所示，
设水柱CD的高度为h．
在Rt△ACD中，∵∠DAC=45°，∴AC=h．
∵∠BAE=30°，∴∠CAB=60°．
在Rt△BCD中，∠CBD=30°，∴ ．
在△ABC中，由余弦定理可得：BC2=AC2+AB2﹣2ACABcos60°．
∴ =h2+1002﹣ ，
化为h2+50h﹣5000=0，解得h=50．
故答案为：50m．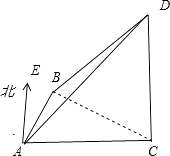

如图所示，设水柱CD的高度为h．在Rt△ACD中，由∠DAC=45°，可得AC=h．由∠BAE=30°，可得∠CAB=60°．在Rt△BCD中，∠CBD=30°，可得 ．在△ABC中，由余弦定理可得：BC2=AC2+AB2﹣2ACABcos60°．代入即可得出．