
【题目】已知函数![]() .
.
(1)当![]() 时,判断
时,判断![]() 是否为
是否为![]() 的极值点,并说明理由;
的极值点,并说明理由;
(2)记![]() .若函数
.若函数![]() 存在极大值
存在极大值![]() ,证明:
,证明:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)将![]() 代入可得
代入可得![]() ,即
,即![]() ,对函数
,对函数![]() 进行求导,令
进行求导,令![]() ,再次进行求导,通过
,再次进行求导,通过![]() 与0的关系,得到
与0的关系,得到![]() 的单调性及最小值为0,即
的单调性及最小值为0,即![]() 恒成立,可得结果;(2)求导可得
恒成立,可得结果;(2)求导可得![]() ,对
,对![]() 进行讨论,分为
进行讨论,分为![]() ,
,![]() ,
,![]() 和
和![]() 四种情形,判断单调性得极值,得其极值
四种情形,判断单调性得极值,得其极值![]() ,再求出
,再求出![]() 的最值即可.
的最值即可.
试题解析:(1)由![]() ,可得
,可得![]() ,故
,故![]() .
.
![]() 不是
不是![]() 的极值点.
的极值点.
理由如下:![]() .
.
记![]() ,则
,则![]() .
.
由![]() ,解得
,解得![]() ;由
;由![]() ,解得
,解得![]() ,
,
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
故![]()
![]() ,即
,即![]() 在
在![]() 恒单调递增,
恒单调递增,
故![]() 不是
不是![]() 的极值点.
的极值点.
(2)依题意,![]() .
.
则![]() .
.
①![]() 时,
时,![]() 在
在![]() 恒成立,
恒成立,![]() 在
在![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上先减后增,故
上先减后增,故![]() 在
在![]() 上有极小值,无极大值,应舍去.
上有极小值,无极大值,应舍去.
②![]() 时,
时,![]() 在
在![]() 恒成立,
恒成立,![]() 在
在![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上先减后增,故
上先减后增,故![]() 在
在![]() 上有极小值,无极大值,应舍去.
上有极小值,无极大值,应舍去.
③![]() 时,由
时,由![]() 得
得![]() 和
和![]() ,
,
|
|
| |
| 大于 | 小于 | 大于 |
| 单调递增 | 单调递减 | 单调递增 |
因为![]() ,故有下列对应关系表:
,故有下列对应关系表:
故![]() ,
,
记![]() ,
,
因为![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() .
.
④当![]() 时,因为
时,因为![]() ,故
,故
|
|
| |
| 大于 | 小于 | 大于 |
| 单调递增 | 单调递减 | 单调递增 |
故![]() ,
,
设![]() ,
,
记![]() ,
,
则![]() ,令
,令![]() 得
得![]() 和
和![]() (舍去),
(舍去),
|
| |
| 小于 | 大于 |
| 单调递减 | 单调递增 |
故![]() .
.


科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每天下雨的概率都为![]() .现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:用
.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:用![]() 表示下雨,从下列随机数表的第
表示下雨,从下列随机数表的第![]() 行第
行第![]() 列的
列的![]() 开始读取,直到读取了
开始读取,直到读取了![]() 组数据,
组数据,
18 18 07 92 45 44 17 16 58 09 79 83 86 19 62 06 76 50 03 10
55 23 64 05 05 26 62 38 97 75 34 16 07 44 99 83 11 46 32 24
据此估计,这三天中恰有两天下雨的概率近似为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医药公司针对某种疾病开发了一种新型药物,患者单次服用制定规格的该药物后,其体内的药物浓度![]() 随时间
随时间![]() 的变化情况(如图所示):当
的变化情况(如图所示):当![]() 时,
时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数);当
为常数);当![]() 时,
时,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数).服药
为常数).服药![]() 后,患者体内的药物浓度为
后,患者体内的药物浓度为![]() ,这种药物在患者体内的药物浓度不低于最低有效浓度,才有疗效;而超过最低中毒浓度,患者就会有危险.
,这种药物在患者体内的药物浓度不低于最低有效浓度,才有疗效;而超过最低中毒浓度,患者就会有危险.
(1)首次服药后,药物有疗效的时间是多长?
(2)首次服药1小时后,可否立即再次服用同种规格的这种药物?
(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
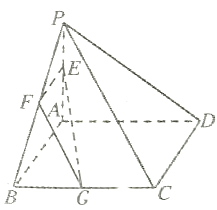
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB,E、F、G分别是PA、PB、BC的中点
(1)证明:平面EFG∥平面PCD;
(2)若平面EFG截四棱锥P-ABCD所得截面的面积为![]() ,求四棱锥P-ABCD的体积
,求四棱锥P-ABCD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 中
中![]() ,
,![]() 为
为![]() 的中点.
的中点.
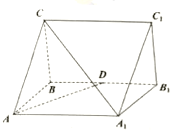
(1)求证:![]() ;
;
(2)若点![]() 为四边形
为四边形![]() 内部及其边界上的点,且三棱锥
内部及其边界上的点,且三棱锥![]() 的体积为三棱柱
的体积为三棱柱![]() 体积的
体积的![]() ,试在图中画出
,试在图中画出![]() 点的轨迹,并说明理由.
点的轨迹,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农业合作社生产了一种绿色蔬菜共![]() 吨,如果在市场上直接销售,每吨可获利
吨,如果在市场上直接销售,每吨可获利![]() 万元;如果进行精加工后销售,每吨可获利
万元;如果进行精加工后销售,每吨可获利![]() 万元,但需另外支付一定的加工费,总的加工
万元,但需另外支付一定的加工费,总的加工![]() (万元)与精加工的蔬菜量
(万元)与精加工的蔬菜量![]() (吨)有如下关系:
(吨)有如下关系: 设该农业合作社将
设该农业合作社将![]() (吨)蔬菜进行精加工后销售,其余在市场上直接销售,所得总利润(扣除加工费)为
(吨)蔬菜进行精加工后销售,其余在市场上直接销售,所得总利润(扣除加工费)为![]() (万元).
(万元).
(1)写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当精加工蔬菜多少吨时,总利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为![]() ,
,![]() .这两条曲线在第一象限的交点为
.这两条曲线在第一象限的交点为![]() ,
,![]() 是以
是以![]() 为底边的等腰三角形.若
为底边的等腰三角形.若![]() ,记椭圆与双曲线的离心率分别为
,记椭圆与双曲线的离心率分别为![]() 、
、![]() ,则
,则![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式: 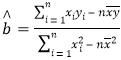 ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com