
| ||
| 4 |
| ||
| 4 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
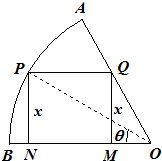 如图,在半径为
如图,在半径为| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为| π | 3 |
查看答案和解析>>
科目:高中数学 来源:南通市二轮天天练(14)(解析版) 题型:解答题
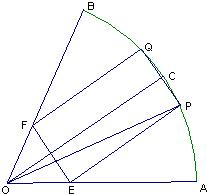
 的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.
的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.
查看答案和解析>>
科目:高中数学 来源: 题型:
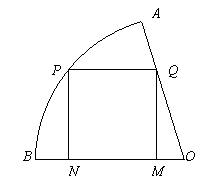 如图,在半径为
如图,在半径为![]() 、圆心角为
、圆心角为![]() 的扇形的弧上任取一点
的扇形的弧上任取一点![]() ,作扇形的内接矩形
,作扇形的内接矩形![]() ,使点
,使点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,设矩形
上,设矩形![]() 的面积为
的面积为![]() ,
,
(1)按下列要求写出函数的关系式:
a.设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
b.设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式,
的函数关系式,
(2)请你选用(1)中的一个函数关系式,求出![]() 的最大值。
的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com