
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)若点![]() 在线段
在线段![]() 上,满足
上,满足![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)证法1:要证明线面平行,转化为证明线线平行,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,证明
,证明![]() ;证法2:要证明线面平行转化为证明面面平行,取
;证法2:要证明线面平行转化为证明面面平行,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,转化为平面
,转化为平面![]() 平面
平面![]() ;(2)取
;(2)取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,易得
,易得![]() ,
,![]() 平面
平面![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,求平面
,求平面![]() 的法向量,利用公式求线面角的正弦值.
的法向量,利用公式求线面角的正弦值.
(Ⅰ)证法1:取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() .
.
![]()
![]() 为
为![]() 中点,
中点,![]()
![]() ,且
,且![]() .
.
又![]() ,且
,且![]() ,
,![]()
![]() ,且
,且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]()
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ;
;
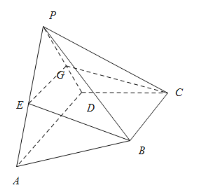
证法2: 取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() .
.
![]()
![]() 为
为![]() 中点,
中点,![]()
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() .
.
又![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]()
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,又
,又![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ;
;
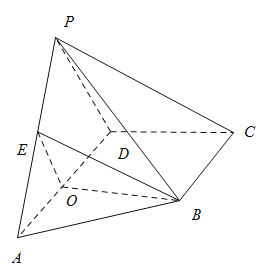
(Ⅱ)取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,
,![]() .
.
![]() ,
,![]() .
.
又平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、
![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,如图所示,
,如图所示,
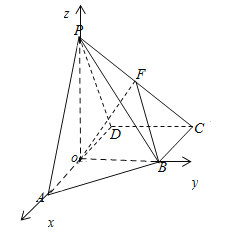
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
, ![]()
![]()
设平面![]() 的法向量
的法向量![]() ,
,
则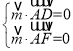 ,
,![]()
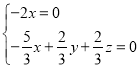 ,
,
得![]() ,取
,取![]() ,则
,则![]() ,
,![]()
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
![]() ,
,
![]()
![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】江苏省高邮市素有“鱼米之乡”之称,高邮城西有风光秀丽的高邮湖,湖内盛产花鲢鱼,记花鲢鱼在湖中的游速为![]() ,花鲢鱼在湖中的耗氧量的单位数为
,花鲢鱼在湖中的耗氧量的单位数为![]() ,经研究花鲢鱼的游速
,经研究花鲢鱼的游速![]() 与
与![]() 成正比,经测定,当花鲢鱼的耗氧量为200单位时,其游速为
成正比,经测定,当花鲢鱼的耗氧量为200单位时,其游速为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式
的函数关系式
(2)计算花鲢鱼静止时耗氧量的单位数.
(3)如果某条花鲢鱼的游速提高了1![]() ,那么它的耗氧量的单位数是原来的多少倍?
,那么它的耗氧量的单位数是原来的多少倍?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对两个变量y和x进行回归分析,则下列说法中不正确的是( )
A.由样本数据得到的回归方程![]() 必过样本点的中心
必过样本点的中心![]() .
.
B.残差平方和越小的模型,拟合的效果越好.
C.用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 的值越小,说明模型的拟合效果越好.
的值越小,说明模型的拟合效果越好.
D.回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 是常数).
是常数).
(1)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(2)若![]() 为奇函数,求实数
为奇函数,求实数![]() .并证明
.并证明![]() 的图像始终在
的图像始终在![]() 的图像的下方;
的图像的下方;
(3)设函数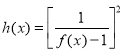 ,若对任意
,若对任意![]() ,以
,以![]() 为边长总可以构成三角形,求
为边长总可以构成三角形,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(I)在答题卡上作出这些数据的频率分布直方图:

(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市工业部门计划对所辖中小型企业推行节能降耗技术改造,下面是对所辖企业是否支持技术改造进行的问卷调查的结果:
支持 | 不支持 | 合计 | |
中型企业 | 40 | ||
小型企业 | 240 | ||
合计 | 560 |
已知从这560家企业中随机抽取1家,抽到支持技术改造的企业的概率为![]() .
.
(1)能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关?
(2)从支持节能降耗的中小企业中按分层抽样的方法抽出8家企业,然后从这8家企业选出2家进行奖励,分别奖励中型企业20万元,小型企业10万元.求奖励总金额为20万元的概率.
附:![]()
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com