
【题目】如图所示,在长方体ABCD﹣A1B1C1D1,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中不成立的是( )

A.EF与BB1垂直B.EF⊥平面BDD1B1
C.EF与C1D所成的角为45°D.EF∥平面A1B1C1D1
【答案】C
【解析】
连A1B,则A1B交AB1于E,可证EF∥A1C1,再由长方体的垂直关系,可判断A正确;由已知可证A1C1⊥平面BDD1B1,可判断B为正确;EF∥A1C1,EF与C1D所成角就是∠A1C1D,∠A1C1D的大小不确定,判断C为错误; EF∥A1C1,可得D正确.
连A1B,则A1B交AB1于E,又F为BC1中点,
可得EF∥A1C1,由B1B⊥平面A1B1C1D1,
可得B1B⊥A1C1,可得B1B⊥EF,故A正确;
由EF∥A1C1,A1C1⊥平面BDD1B1,
可得EF⊥平面BDD1B1,故B正确;
EF与C1D所成角就是∠A1C1D,∵AA1 的长度不确定,
∴∠A1C1D的大小不确定,故C错误;
由E,F分别是AB1,BC1的中点,
得EF∥A1C1,可得EF∥平面A1B1C1D1,故D正确.
故选:C.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】画糖是一种以糖为材料在石板上进行造型的民间艺术,常见于公园与旅游景点.某师傅制作了一种新造型糖画,为了进行合理定价先进性试销售,其单价![]() (元)与销量
(元)与销量![]() (个)相关数据如下表:
(个)相关数据如下表:

(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性相关方程;
的线性相关方程;
(2)若该新造型糖画每个的成本为![]() 元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
参考公式:线性回归方程![]() 中斜率和截距最小二乘法估计计算公式:
中斜率和截距最小二乘法估计计算公式:

![]() .参考数据:
.参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的![]() ,
,![]() ,
,![]() 三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
车间 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() ,
,![]() ,
,![]() 各车间产品的数量;
各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件产品来自相同车间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】篮球运动于1891年起源于美国,它是由美国马萨诸塞州斯普林菲尔德(旧译麻省春田)市基督教青年会(![]() )训练学校的体育教师詹姆士·奈史密斯博士(
)训练学校的体育教师詹姆士·奈史密斯博士(![]() )发明.它是以投篮、上篮和扣篮为中心的对抗性体育运动之一,是可以增强体质的一种运动.已知篮球的比赛中,得分规则如下:3分线外侧投入可得3分,3分线内侧投入可得2分,不进得0分.经过多次试验,某人投篮100次,有20个是3分线外侧投入,30个是3分线内侧投入,其余不能入篮,且每次投篮为相互独立事件.
)发明.它是以投篮、上篮和扣篮为中心的对抗性体育运动之一,是可以增强体质的一种运动.已知篮球的比赛中,得分规则如下:3分线外侧投入可得3分,3分线内侧投入可得2分,不进得0分.经过多次试验,某人投篮100次,有20个是3分线外侧投入,30个是3分线内侧投入,其余不能入篮,且每次投篮为相互独立事件.
(1)求该人在4次投篮中恰有三次是3分线外侧投入的概率;
(2)求该人在4次投篮中至少有一次是3分线外侧投入的概率;
(3)求该人两次投篮后得分![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
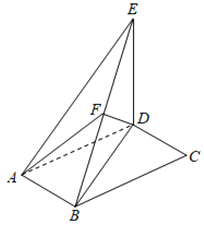
(1)求证:AB⊥DE;
(2)若点F为BE的中点,求直线AF与平面ADE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P在曲线x2+y2=1上运动,过点P作x轴的垂线,垂足为Q,动点M满足![]() .
.
(1)求动点M的轨迹方程;
(2)点AB在直线x﹣y﹣4=0上,且AB=4,求△MAB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C:![]() (a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足
(a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足![]() ,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
A. B.
B.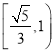
C.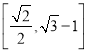 D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com