
| Sn |
| n |
| 1 |
| 2 |
| an |
| an+2011 |
| n |
| n+2011 |
| k(q+2011) |
| q-k |
| Sn |
| n |
| 3n+1 |
| 2n-1 |
| 3n+1 |
| 2n-1 |
| 3n+2+1 |
| 2n+3 |
| 3n+1 |
| 2n-1 |
| -4(4n-3)3n+4 |
| (2n-1)(2n+3) |
| 3n-1 |
| 2n-1 |
| 3n-1 |
| 2n-1 |
| 3n+2-1 |
| 2n+3 |
| 3n-1 |
| 2n-1 |
| 4(4n-3)3n+4 |
| (2n-1)(2n+3) |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| n |
| n+2011 |
| k |
| k+2011 |
| p |
| p+2011 |
| q |
| q+2011 |
| k(q+2011) |
| q-k |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
| an |
| an+2012 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
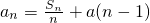 ��
��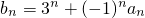 ��������{bn}�ǵ����������У���ʵ��a��ȡֵ��Χ��
��������{bn}�ǵ����������У���ʵ��a��ȡֵ��Χ�� ������{cn}���㣺
������{cn}���㣺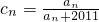 ���������������������k���Ƿ����p��q��N*��ʹck=cp•cq�������ڣ���p��q��ֵ��ֻҪд��һ�鼴�ɣ����������ڣ�˵�����ɣ�
���������������������k���Ƿ����p��q��N*��ʹck=cp•cq�������ڣ���p��q��ֵ��ֻҪд��һ�鼴�ɣ����������ڣ�˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012-2013ѧ�꽭��ʡ��Ǩ����������Զ��ѧ��һ���ϣ���һ�ν�ѧ���������ѧ�Ծ��������ࣩ�������棩 ���ͣ������
 ��
�� �������������n���������ʵ��a��ȡֵ��Χ��
�������������n���������ʵ��a��ȡֵ��Χ�� ������{cn}���㣺
������{cn}���㣺 ���������������������k���Ƿ����p��q��N*��ʹ��ck=cp•cq�������ڣ����p��q��ֵ��ֻҪд��һ�鼴�ɣ�����������˵�����ɣ�
���������������������k���Ƿ����p��q��N*��ʹ��ck=cp•cq�������ڣ����p��q��ֵ��ֻҪд��һ�鼴�ɣ�����������˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ�꽭��ʡ�������������˺���ѧ�������ϣ�12��ѧ�������ѧ�Ծ���1���������棩 ���ͣ������
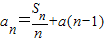 ��
�� ��������{bn}�ǵ����������У���ʵ��a��ȡֵ��Χ��
��������{bn}�ǵ����������У���ʵ��a��ȡֵ��Χ��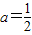 ������{cn}���㣺
������{cn}���㣺 ���������������������k���Ƿ����p��q��N*��ʹck=cp•cq�������ڣ���p��q��ֵ��ֻҪд��һ�鼴�ɣ����������ڣ�˵�����ɣ�
���������������������k���Ƿ����p��q��N*��ʹck=cp•cq�������ڣ���p��q��ֵ��ֻҪд��һ�鼴�ɣ����������ڣ�˵�����ɣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com