
【题目】对于函数![]() ,若存在实数m,使得
,若存在实数m,使得![]() 为R上的奇函数,则称
为R上的奇函数,则称![]() 是位差值为m的“位差奇函数”.
是位差值为m的“位差奇函数”.
(1)判断函数![]() 和
和![]() 是否是位差奇函数,并说明理由;
是否是位差奇函数,并说明理由;
(2)若![]() 是位差值为
是位差值为![]() 的位差奇函数,求
的位差奇函数,求![]() 的值;
的值;
(3)若对于任意![]() ,
,![]() 都不是位差值为m的位差奇函数,求实数t的取值范围.
都不是位差值为m的位差奇函数,求实数t的取值范围.
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与抛物线的另一个交点为
与抛物线的另一个交点为![]() ,直线
,直线![]() 与抛物线的另一个交点为
与抛物线的另一个交点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系上,有一点列![]() ,设点
,设点![]() 的坐标
的坐标![]() (
(![]() ),其中
),其中![]() . 记
. 记![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)已知点![]() ,点
,点![]() 满足
满足![]() ,求
,求![]() 的坐标;
的坐标;
(2)已知点![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是递增数列,点
)是递增数列,点![]() 在直线
在直线![]() :
:![]() 上,求
上,求![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年6月,国内的![]() 运营牌照开始发放.从
运营牌照开始发放.从![]() 到
到![]() ,我们国家的移动通信业务用了不到20年的时间,完成了技术上的飞跃,跻身世界先进水平.为了解高校学生对
,我们国家的移动通信业务用了不到20年的时间,完成了技术上的飞跃,跻身世界先进水平.为了解高校学生对![]() 的消费意愿,2019年8月,从某地在校大学生中随机抽取了1000人进行调查,样本中各类用户分布情况如下:
的消费意愿,2019年8月,从某地在校大学生中随机抽取了1000人进行调查,样本中各类用户分布情况如下:
用户分类 | 预计升级到 | 人数 |
早期体验用户 | 2019年8月至2019年12月 | 270人 |
中期跟随用户 | 2020年1月至2021年12月 | 530人 |
后期用户 | 2022年1月及以后 | 200人 |
我们将大学生升级![]() 时间的早晚与大学生愿意为
时间的早晚与大学生愿意为![]() 套餐支付更多的费用作比较,可得出下图的关系(例如早期体验用户中愿意为
套餐支付更多的费用作比较,可得出下图的关系(例如早期体验用户中愿意为![]() 套餐多支付5元的人数占所有早期体验用户的
套餐多支付5元的人数占所有早期体验用户的![]() ).
).

(1)从该地高校大学生中随机抽取1人,估计该学生愿意在2021年或2021年之前升级到![]() 的概率;
的概率;
(2)从样本的早期体验用户和中期跟随用户中各随机抽取1人,以![]() 表示这2人中愿意为升级
表示这2人中愿意为升级![]() 多支付10元或10元以上的人数,求
多支付10元或10元以上的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
![]() 套餐,能否认为样本中早期体验用户的人数有变化?说明理由.
套餐,能否认为样本中早期体验用户的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AD=2.
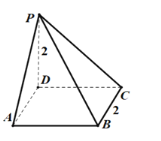
(1)求该四棱锥P-ABCD的表面积和体积;
(2)求该四棱锥P-ABCD内切球的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在年终“尾牙”宴上对该公司年度的最佳销售员工进行奖励,已知员工![]() 一年以来的月销售业绩分别为:102,113,123,132,144,138,126,119,108,122,109,146.若该公司为最佳员工准备了相应的奖品,需要该员工通过抽奖游戏进行确定奖品金额,游戏规则如下:该员工需要从9张卡牌中不放回的抽取3张,其中1张卡牌的奖金为600元,4张卡牌的奖金均为400元,另外4张卡牌的奖金均为200元,所抽到的3张卡牌的金额之和
一年以来的月销售业绩分别为:102,113,123,132,144,138,126,119,108,122,109,146.若该公司为最佳员工准备了相应的奖品,需要该员工通过抽奖游戏进行确定奖品金额,游戏规则如下:该员工需要从9张卡牌中不放回的抽取3张,其中1张卡牌的奖金为600元,4张卡牌的奖金均为400元,另外4张卡牌的奖金均为200元,所抽到的3张卡牌的金额之和![]() 便是该员工所获得的奖品的最终价值.
便是该员工所获得的奖品的最终价值.
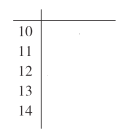
(Ⅰ)请根据题意完善员工![]() 的业绩的茎叶图,并求出员工
的业绩的茎叶图,并求出员工![]() 销售业绩的中位数;
销售业绩的中位数;
(Ⅱ)求![]() 的分布列以及数学期望.
的分布列以及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com