
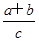 的取值范围是
的取值范围是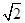 ) C.(1,
) C.(1,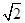 ] D.[1,
] D.[1, ]
] 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源:不详 题型:解答题
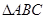 的两边长分别为
的两边长分别为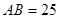 ,
,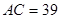 ,且O为
,且O为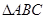 外接圆的圆心.(注:
外接圆的圆心.(注: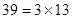 ,
,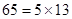 )
)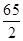 ,且角B为钝角,求BC边的长;
,且角B为钝角,求BC边的长;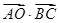 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
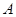 处获悉,其正东方向20海里
处获悉,其正东方向20海里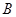 处有一艘渔船遇险等待营救,此时救援船在港口的南偏西
处有一艘渔船遇险等待营救,此时救援船在港口的南偏西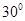 据港口10海里的
据港口10海里的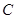 处,救援船接到救援命令立即从
处,救援船接到救援命令立即从 处沿直线前往
处沿直线前往 处营救渔船.
处营救渔船.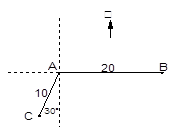
 处应朝北偏东多少度的方向沿直线前往
处应朝北偏东多少度的方向沿直线前往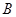 处救援?(已知
处救援?(已知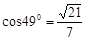 ).
).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com