
 是偶函数;
是偶函数; 是函数
是函数 图象的一条对称轴;
图象的一条对称轴; 在
在 上是单调增函数;
上是单调增函数; 是函数
是函数 图象的对称中心.
图象的对称中心.| A.①②③ | B.②③④ | C.②④ | D.③④ |
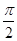 ),再判断其奇偶性;然后利用y=sinx的对称轴是使函数值等于1时的x的值,其单调区间是[-
),再判断其奇偶性;然后利用y=sinx的对称轴是使函数值等于1时的x的值,其单调区间是[- 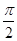 +2kπ,
+2kπ,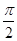 +2kπ,k∈N+]来判断②③,另外正切函数的对称中心是使函数值为0的x的值,可判断④.
+2kπ,k∈N+]来判断②③,另外正切函数的对称中心是使函数值为0的x的值,可判断④.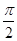 )=sin(-x)=-sinx,所以①为奇函数;
)=sin(-x)=-sinx,所以①为奇函数;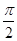 +kπ,令2x+
+kπ,令2x+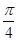 =
=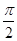 +kπ,x=
+kπ,x=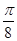 +
+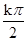 ,当k=0时,x=
,当k=0时,x=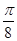 ,所以②正确;
,所以②正确;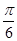 )的递增区间为-
)的递增区间为-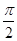 +2kπ≤x+
+2kπ≤x+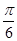 ≤
≤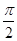 +2kπ,得-
+2kπ,得- +2kπ≤ x ≤
+2kπ≤ x ≤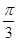 + 2kπ,(-
+ 2kπ,(-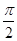 ,
,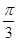 )在该区间范围内,所以③正确;
)在该区间范围内,所以③正确;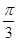 )的对称中心为(k
)的对称中心为(k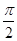 +
+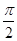 ,0), 当x+
,0), 当x+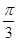 =
=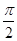 时,x=
时,x=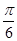 ,所以④正确,故答案为B.
,所以④正确,故答案为B.

科目:高中数学 来源:不详 题型:单选题
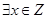 ,x2+x+m<0”的否定是( )
,x2+x+m<0”的否定是( )| A.存在x∈Z使x2+x+m≥0 |
B.不存在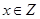 使x2+x+m≥0 使x2+x+m≥0 |
C.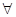 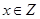 ,x2+x+m≤0 ,x2+x+m≤0 |
D.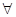 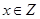 ,x2+x+m≥0 ,x2+x+m≥0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
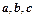 ,若a∥b,b∥c,则a∥c;
,若a∥b,b∥c,则a∥c;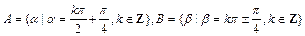 ,则
,则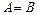 ;
;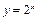 的图象与函数
的图象与函数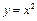 的图象有且仅有
的图象有且仅有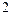 个公共点;
个公共点;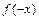 的图象向右平移2个单位,得到
的图象向右平移2个单位,得到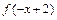 的图象.
的图象.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
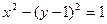 按
按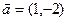 平移可得曲线
平移可得曲线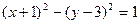 ;
;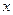 -1|+|
-1|+|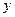 -1|
-1|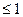 ,则使
,则使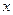
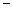
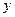 取得最小值的最优解有无数多个;
取得最小值的最优解有无数多个;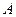 、
、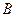 为两个定点,
为两个定点,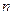 为
为 常数,
常数,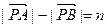 ,则动点
,则动点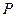 的轨迹为双曲线;
的轨迹为双曲线;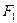 、
、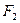 ,
,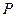 是该椭圆上的任意一点,延长
是该椭圆上的任意一点,延长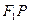 到点
到点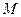 ,使
,使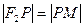 ,则点
,则点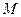 的轨迹是圆.
的轨迹是圆.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com