[题目]下列说法中错误的是( )A.将一组数据中的每一个数据都加上或减去同一个常数后.方差不变B.设有一个线性回归方程.变量x增加1个单位时.y平均增加5个单位C.设具有相关关系的两个变量x.y的相关系数为r.则越接近于0.x和y之间的线性相关程度越强D.在一个列联表中.由计算得的值.则的值越大.判断两个变量间有关联的把握就越大题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】下列说法中错误的是（）

A.将一组数据中的每一个数据都加上或减去同一个常数后，方差不变

B.设有一个线性回归方程，变量x增加1个单位时，y平均增加5个单位

C.设具有相关关系的两个变量x，y的相关系数为r，则越接近于0，x和y之间的线性相关程度越强

D.在一个列联表中，由计算得的值，则的值越大，判断两个变量间有关联的把握就越大

【答案】BC

【解析】

根据回归方程的特征，相关系数的概念及的意义，逐一分析四个答案的正误，可得答案.

对于A：方差反映一组数据的波动情况，将一组数据中每一个数据都加上或减去同一个常数后，波动情况不变，方差不变，故A正确；

对于B：线性回归方程，变量x增加1个单位时，y平均减少5个单位，故B错误；

对于C：相关系数越接近于0，相关性越弱，关系数越接近于1，相关性越强，故C错误；

对于D：的值越大，x与y有关系的可信度越大，两个变量间有关联的把握就越大，故D正确.

故选：BC.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某次测验，将20名学生平均分为两组，测验结果两组学生成绩的平均分和标准差分别为90，6；80，4．则这20名学生成绩的方差为_____．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（1）已知扇形的周长为8，面积是4，求扇形的圆心角．

（2）已知扇形的周长为40，当它的半径和圆心角取何值时，才使扇形的面积最大？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】随着“中华好诗词”节目的播出，掀起了全民诵读传统诗词经典的热潮.某社团为调查大学生对于“中华诗词”的喜好，从甲、乙两所大学各随机抽取了40名学生，记录他们每天学习“中华诗词”的时间，并整理得到如下频率分布直方图：

根据学生每天学习“中华诗词”的时间，可以将学生对于“中华诗词”的喜好程度分为三个等级 :

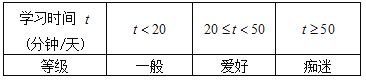
(Ⅰ)从甲大学中随机选出一名学生，试估计其“爱好”中华诗词的概率；

(Ⅱ)从两组“痴迷”的同学中随机选出2人，记为选出的两人中甲大学的人数，求的分布列和数学期望；

(Ⅲ)试判断选出的这两组学生每天学习“中华诗词”时间的平均值与的大小，及方差与的大小．(只需写出结论)

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数.

（1）当时，讨论函数的单调性；

（2）若函数在区间上无零点，求的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为响应“文化强国建设”号召，并增加学生们对古典文学的学习兴趣，雅礼中学计划建设一个古典文学熏陶室.为了解学生阅读需求，随机抽取200名学生做统计调查.统计显示，男生喜欢阅读古典文学的有64人，不喜欢的有56人；女生喜欢阅读古典文学的有36人，不喜欢的有44人.

(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系？

(2)为引导学生积极参与阅读古典文学书籍，语文教研组计划牵头举办雅礼教育集团古典文学阅读交流会.经过综合考虑与对比，语文教研组已经从这200人中筛选出了5名男生代表和4名女生代表，其中有3名男生代表和2名女生代表喜欢古典文学.现从这9名代表中任选3名男生代表和2名女生代表参加交流会，记为参加交流会的5人中喜欢古典文学的人数，求的分布列及数学期望.