练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线l过抛物线C的焦点，且与C的对称轴垂直．l与C交于A，B两点，|AB|=12，P为C的准线上一点，则△ABP的面积为（ ）
    A.18
    B.24
    C.36
    D.48

    【答案】C
    【解析】解：设抛物线的解析式为y2=2px（p＞0）， 则焦点为F（ ，0），对称轴为x轴，准线为x=﹣
    ∵直线l经过抛物线的焦点，A、B是l与C的交点，
    又∵AB⊥x轴
    ∴|AB|=2p=12
    ∴p=6
    又∵点P在准线上
    ∴DP=（ +|﹣ |）=p=6
    ∴S△ABP= （DPAB）= ×6×12=36
    故选C．

    首先设抛物线的解析式y2=2px（p＞0），写出次抛物线的焦点、对称轴以及准线，然后根据通径|AB|=2p，求出p，△ABP的面积是|AB|与DP乘积一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，若，且，则的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知甲、乙两组数据的茎叶如图所示，若它们的平均数相同，则下列关于甲、乙两组数据稳定性的描述，正确的是（ ）
    A.甲较稳定
    B.乙较稳定
    C.二者相同
    D.无法判断

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为迎接党的“十九”大的召开，某校组织了“歌颂祖国，紧跟党走”党史知识竞赛，从参加考试的学生中抽出50名学生，将其成绩（满分100分，成绩均为整数）分成六段， ，…， 后绘制频率分布直方图（如下图所示）

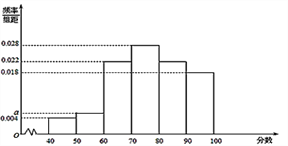
    （Ⅰ）求频率分布图中的值；

    （Ⅱ）估计参加考试的学生得分不低于80的概率；

    （Ⅲ）从这50名学生中，随机抽取得分在的学生2人，求此2人得分都在的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数.

    （1）求的单调区间；

    （2）若，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，侧面底面， ， ， ， ， 分别为， 的中点．

    （1）求证： 平面；

    （2）求证： 平面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2sin Acos C=2sin B-sin C.

    (1)求A的大小;

    (2)在锐角三角形ABC中, ，求c+b的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y=2x2﹣2x﹣3有以下4个结论： ①定义域为R，
    ②递增区间为[1，+∞）
    ③是非奇非偶函数；
    ④值域是[ ，∞）．
    其中正确的结论是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=﹣ x3+ x2﹣6x+5的单调增区间是（ ）
    A.（﹣∞，2）和（3，+∞）
    B.（2，3）
    C.（﹣1，6）
    D.（﹣3，﹣2）

    查看答案和解析>>

    同步练习册答案