
【题目】已知f(x)=xex﹣ax2﹣x,a∈R.
(1)当a= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)若对x≥1时,恒有f(x)≥xex+ax2成立,求实数a的取值范围.
【答案】
(1)解:f′(x)=(x+1)ex﹣2ax﹣1,
当a= ![]() 时,f′(x)=(x+1)ex﹣(x+1)=(x+1)(ex﹣1),
时,f′(x)=(x+1)ex﹣(x+1)=(x+1)(ex﹣1),
当x>0或x<﹣1时,f′(x)>0,当﹣1<x<0时,f′(x)<0,
函数f(x)的单调递增区间为(﹣∞,﹣1),(0,+∞),单调递减区间为(﹣1,0);
(2)解:若对x≥1时,恒有f(x)≥xex+ax2成立,
即g(x)=ax2+x在≤0[1,+∞)恒成立,
①a=0时,g(x)=x,显然不成立,
②故a<0,g(x)=ax2+x开口向下,对称轴x=﹣ ![]() ,
,
﹣ ![]() <1即a<﹣
<1即a<﹣ ![]() 时,g(x)在[1,+∞)递减,
时,g(x)在[1,+∞)递减,
g(x)min=g(1)=a+1≤0,解得:a≤﹣1;
﹣ ![]() ≤a<0时,g(x)在[1,﹣
≤a<0时,g(x)在[1,﹣ ![]() )递增,在(﹣
)递增,在(﹣ ![]() ,+∞)递减,
,+∞)递减,
g(x)max=g(﹣ ![]() )=﹣
)=﹣ ![]() >0,不成立,
>0,不成立,
综上:a≤﹣1.
【解析】(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)问题转化为g(x)=ax2+x在≤0[1,+∞)恒成立,a=0时,不成立,a<0时,结合二次函数的性质求出a的范围即可.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】下列各组函数f(x)与g(x)的图象相同的是( )
A.f(x)=x,g(x)=( ![]() )2
)2
B.f(x)=x2 , g(x)=(x+1)2
C.f(x)=1,g(x)=x0
D.f(x)=|x|,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆E:(x+ ![]() )2+y2=16,点F(
)2+y2=16,点F( ![]() ,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q. 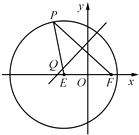
(1)求动点Q的轨迹Γ的方程;
(2)设直线l与(1)中轨迹Γ相交于A,B两点,直线AO,l,OB的斜率分别为k1 , k,k2(其中k>0),若k1 , k,k2恰好构成公比不为1的等比数列,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得的数据整理后,画频率分布直方图.已知图中横轴从左向右的分组为[50,75)、[75,100)、[100,125)、[125,150],纵轴前3个对应值分别为0.004、0.01、0.02,因失误第4个对应值丢失. 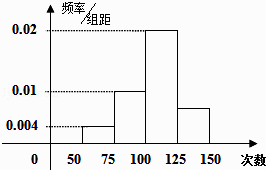
(Ⅰ) 已知第1小组频数为10,求参加这次测试的人数?
(Ⅱ) 求第4小组在y轴上的对应值;
(Ⅲ) 若次数在75次以上 ( 含75次 ) 为达标,试估计该年级跳绳测试达标率是多少?
(Ⅳ) 试估计这些数据的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2ax(a为实数),且f(1)= ![]() .
.
(1)求函数f(x)的解析式;
(2)判断函数f(x)的奇偶性并证明;
(3)判断函数f(x)在区间[0,+∞)的单调性,并用定义证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com