
����Ŀ��Ϊ�˼��ij�ֲ�Ʒ����������λ��ǧ�ˣ�����ȡ��һ������ΪN�������������õ�������������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ��ͼ��
���� | Ƶ�� | Ƶ�� |
[17.5��20�� | 10 | 0.05 |
[20��225�� | 50 | 0.25 |
[22.5��25�� | a | b |
[25��27.5�� | 40 | c |
[27.5��30] | 20 | 0.10 |
�ϼ� | N | 1 |
�����������N��a��b��c��ֵ��
������Ƶ�ʷֲ�ֱ��ͼ��d��ֵ��
���Ӹò�Ʒ�������ȡһ�����Թ��������Ʒ����������25ǧ�˵ĸ��ʣ�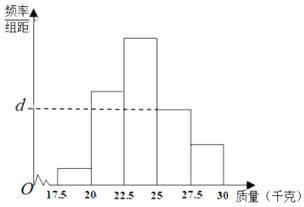
���𰸡��⣺������Ƶ�ʷֲ����ã�
 ��
��
���N=200��a=80��b=0.4��c=0.2��
������Ƶ�ʷֲ�����[25��27.5��Ƶ��Ϊ0.2��
��d= ![]() =0.08��
=0.08��
������Ƶ�ʷֲ���֪��Ʒ������������25ǧ�˵�Ƶ��Ϊ0.2+0.1=0.3��
��Ӹò�Ʒ�������ȡһ����
���������Ʒ����������25ǧ�˵ĸ���p=1��0.3=0.7
��������������Ƶ��= ![]() ����Ƶ�ʷֲ������������N��a��b��c��ֵ��������Ƶ�ʷֲ�����[25��27.5��Ƶ��Ϊ0.2���ɴ������Ƶ�ʷֲ�ͼ�е�d��ֵ��������Ƶ�ʷֲ���֪��Ʒ������������25ǧ�˵�Ƶ��Ϊ0.2+0.1=0.3���Ӹò�Ʒ�������ȡһ�����ɴ��ܹ��������Ʒ����������25ǧ�˵ĸ��ʣ�
����Ƶ�ʷֲ������������N��a��b��c��ֵ��������Ƶ�ʷֲ�����[25��27.5��Ƶ��Ϊ0.2���ɴ������Ƶ�ʷֲ�ͼ�е�d��ֵ��������Ƶ�ʷֲ���֪��Ʒ������������25ǧ�˵�Ƶ��Ϊ0.2+0.1=0.3���Ӹò�Ʒ�������ȡһ�����ɴ��ܹ��������Ʒ����������25ǧ�˵ĸ��ʣ�
�����㾫����������Ĺؼ���������Ƶ�ʷֲ��������֪ʶ�����յ�һ������ڶ����������������������������ȷ���ֵ㣬�����ݷ��飻���IJ�����Ƶ�ʷֲ������Լ���Ƶ�ʷֲ�ֱ��ͼ�����⣬�˽�Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��F1��F2��˫���� ![]() =1��a��0�������ҽ��㣬��F1��ֱ��l��˫���߽��ڵ�A��B������ABF2Ϊ�ȱ������Σ����BF1F2�����Ϊ�� ��
=1��a��0�������ҽ��㣬��F1��ֱ��l��˫���߽��ڵ�A��B������ABF2Ϊ�ȱ������Σ����BF1F2�����Ϊ�� �� 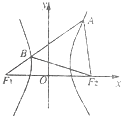
A.8
B.8 ![]()
C.8 ![]()
D.16
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У�A(2����1)��B(4,3)��C(3����2)��
��1����BC���ϵĸ�����ֱ�ߵ�һ��ʽ���̣�
��2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}����a1= ![]() ��an+1=a
��an+1=a ![]() ��an+1����M=
��an+1����M= ![]() +
+ ![]() +��+
+��+ ![]() �����������ǣ� ��
�����������ǣ� ��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊ�˶�һ���²�Ʒ���к������ۣ����ò�Ʒ���~���ⶨ�ļ۸�����������õ��������ݣ�
����x��Ԫ�� | 4 | 5 | 6 | 7 | 8 | 9 |
����V������ | 90 | 84 | 83 | 80 | 75 | 68 |
�ɱ������ݣ�������Իع鷽��Ϊ ![]() =��4x+a��������Щ����������ȡһ�㣬�t���ڻع�ֱ�����Ϸ��ĸ���Ϊ
=��4x+a��������Щ����������ȡһ�㣬�t���ڻع�ֱ�����Ϸ��ĸ���Ϊ
�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������P��ABCD�У��ı���ABCDΪ���Σ���PADΪ���������Σ���APD=90�㣬ƽ��PAD��ƽ��ABCD����AB=1��AD=2��E��F�ֱ�ΪPC��BD���е㣮 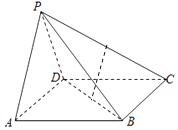
��1��֤����EF��ƽ��PAD��
��2��֤����ֱ��PA��ƽ��PCD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������װ��2������4��������ɫ�⣬���ǵ���״����С����������ȫ��ͬ.
��1�����ò��Żس������Ⱥ�ȡ���Σ�ÿ�����ȡһ������ǡ��ȡ��1������1������ĸ��ʣ�
��2�����÷Żس�����ÿ�����ȡһ������ȡ5�Σ���ǡ������ȡ������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}������Ϊ1��SnΪ����{an}��ǰn��ͣ�Sn+1=qSn+1������q��0��n��N* ��
��1����2a2 �� a3 �� a2+2�ɵȲ����У�������{an}��ͨ�ʽ��
��2��������{bn}����bn= ![]() ����b2=
����b2= ![]() ��֤����b1+b2+��+bn��
��֤����b1+b2+��+bn�� ![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com