
【题目】某工厂36名工人年龄数据如图:
工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 |
1 | 40 | 10 | 36 | 19 | 27 | 28 | 34 |
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的均值 ![]() 和方差s2;
和方差s2;
(3)36名工人中年龄在 ![]() ﹣s和
﹣s和 ![]() +s之间有多少人?所占百分比是多少(精确到0.01%)?
+s之间有多少人?所占百分比是多少(精确到0.01%)?
【答案】
(1)解:由系统抽样知,36人分成9组,每组4人,其中第一组的工人年龄为44,所以其编号为2,
∴所有样本数据的编号为:4n﹣2,(n=1,2,…,9),
其数据为:44,40,36,43,36,37,44,43,37
(2)解:由平均值公式得 ![]() =
= ![]() (44+40+36+43+36+37+44+43+37)=40.
(44+40+36+43+36+37+44+43+37)=40.
由方差公式得s2= ![]() [(44﹣40)2+(40﹣40)2+…+(37﹣40)2]=
[(44﹣40)2+(40﹣40)2+…+(37﹣40)2]= ![]()
(3)解:∵s2= ![]() .∴s=
.∴s= ![]() ∈(3,4),
∈(3,4),
∴36名工人中年龄在 ![]() ﹣s和
﹣s和 ![]() +s之间的人数等于区间[37,43]的人数,
+s之间的人数等于区间[37,43]的人数,
即40,40,41,…,39,共23人.
∴36名工人中年龄在 ![]() ﹣s和
﹣s和 ![]() +s之间所占百分比为
+s之间所占百分比为 ![]() ≈63.89%
≈63.89%
【解析】(1)利用系统抽样的定义进行求解即可;(2)根据均值和方差公式即可计算(1)中样本的均值 ![]() 和方差s2;(3)求出样本和方差即可得到结论.
和方差s2;(3)求出样本和方差即可得到结论.
【考点精析】根据题目的已知条件,利用系统抽样方法和极差、方差与标准差的相关知识可以得到问题的答案,需要掌握把总体的单位进行排序,再计算出抽样距离,然后按照这一固定的抽样距离抽取样本;第一个样本采用简单随机抽样的办法抽取;标准差和方差越大,数据的离散程度越大;标准差和方程为0时,样本各数据全相等,数据没有离散性;方差与原始数据单位不同,解决实际问题时,多采用标准差.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1=λan+2n(n∈N* , λ∈R),且a1=2.
(1)若λ=1,求数列{an}的通项公式;
(2)若λ=2,证明数列{ ![]() }是等差数列,并求数列{an}的前n项和Sn .
}是等差数列,并求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过不重合的A(m2+2,m2﹣3),B(3﹣m﹣m2 , 2m)两点的直线l倾斜角为45°,则m的取值为( )
A.m=﹣1
B.m=﹣2
C.m=﹣1或2
D.m=l或m=﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+1满足f(﹣1)=0,且x∈R时,f(x)的值域为[0,+∞).
(1)求f(x)的表达式;
(2)设函数g(x)=f(x)﹣2kx,k∈R. ①若g(x)在x∈[﹣2,2]时是单调函数,求实数k的取值范围;
②若g(x)在x∈[﹣2,2]上的最小值g(x)min=﹣15,求k值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点,设异面直线EM与AF所成的角为θ,则cosθ的最大值为 . 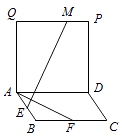
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:以点 ![]() 为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为原点,
为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为原点,
(1)求证:△OAB的面积为定值;
(2)设直线y=﹣2x+4与圆C交于点M,N,若OM=ON,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,Sn表示数列{an}的前n项的和,且 ![]()
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,实轴长为2,直线l:x﹣y+m=0与双曲线C交于不同的两点A,B,
,实轴长为2,直线l:x﹣y+m=0与双曲线C交于不同的两点A,B,
(1)求双曲线C的方程;
(2)若线段AB的中点在圆x2+y2=5上,求m的值;
(3)若线段AB的长度为4 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com