
已知各项均为正数的数列{a }满足a
}满足a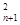 =2a
=2a +a
+a a
a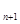 ,且a
,且a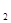 +a
+a =2a
=2a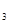 +4,其中n∈N
+4,其中n∈N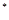 .
.
(Ⅰ)若b =
=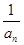 ,求数列{b
,求数列{b }的通项公式;
}的通项公式;
(Ⅱ)证明: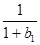 +
+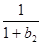 +…+
+…+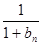 >
>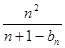 (n≥2).
(n≥2).
(1)b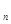 =
=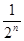 (n∈N
(n∈N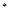 )
)
(2)构造函数借助于函数的最值来证明不等式。
【解析】
试题分析:解:(Ⅰ)因为a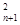 =2a
=2a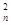 +a
+a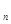 a
a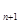 ,即(a
,即(a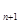 +a
+a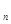 )(2a
)(2a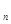 -a
-a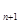 )=0.
1分
)=0.
1分
又a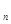 >0,所以有2a
>0,所以有2a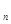 -a
-a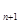 =0,即2a
=0,即2a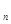 =a
=a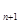
所以数列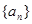 是公比为2的等比数列,
3分
是公比为2的等比数列,
3分
由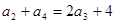 得
得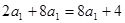 ,解得
,解得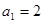 。
。
从而,数列{a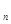 }的通项公式为a
}的通项公式为a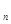 =2
=2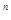 (n∈N
(n∈N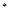 ),即:b
),即:b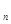 =
=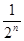 (n∈N
(n∈N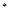 ). 5分
). 5分
(Ⅱ)构造函数f(x)=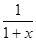 -
-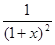 (b
(b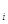 -x)(x>0),
-x)(x>0),
则f′(x)=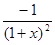 -
-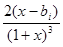 +
+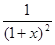 =
=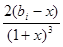 ,
,
当0<x<b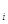 时,f′(x)>0,x>b
时,f′(x)>0,x>b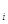 时,f′(x)<0,
时,f′(x)<0,
所以f(x)的最大值是f(b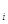 )=
)=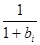 ,所以f(x)≤
,所以f(x)≤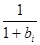 .
7分
.
7分
即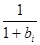 ≥
≥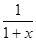 -
-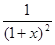 (b
(b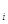 -x)(x>0,i=1,2,3…n),取“=”的条件是x=b
-x)(x>0,i=1,2,3…n),取“=”的条件是x=b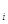 (i=1,2,3…n),
(i=1,2,3…n),
所以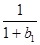 +
+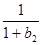 +…+
+…+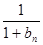 >
>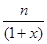 -
-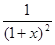 (b
(b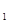 +b
+b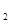 +…+b
+…+b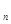 -nx), 9分
-nx), 9分
令x=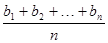 ,则
,则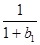 +
+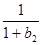 +…+
+…+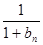 >
> ,
,
所以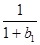 +
+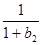 +…+
+…+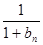 >
>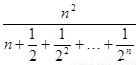 ,
11分
,
11分
即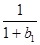 +
+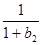 +…+
+…+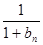 >
>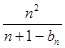 (n≥2).
12分
(n≥2).
12分
考点:数列与导数、不等式
点评:解决的关键是能利用等比数列来求解通项公式,同时能结合导数来拍脑袋函数单调性,以及求解函数的最值,同时证明不等式,属于中档题。


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
| Tn+1+12 |
| 4Tn |
| 2log2bn+1+2 |
| 2log2bn-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 与
与 的大小,并加以证明.
的大小,并加以证明.查看答案和解析>>
科目:高中数学 来源:青岛二模 题型:解答题
| Tn+1+12 |
| 4Tn |
| 2log2bn+1+2 |
| 2log2bn-1 |
查看答案和解析>>
科目:高中数学 来源:《第2章 数列》、《第3章 不等式》2010年单元测试卷(陈经纶中学)(解析版) 题型:解答题
 与
与 的大小,并加以证明.
的大小,并加以证明.查看答案和解析>>
科目:高中数学 来源:2012年高考复习方案配套课标版月考数学试卷(二)(解析版) 题型:解答题
 与
与 的大小,并加以证明.
的大小,并加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com