练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知a＞0，且a≠1，则双曲线C1： ﹣y2=1与双曲线C2： ﹣x2=1的（ ）
    A.焦点相同
    B.顶点相同
    C.渐近线相同
    D.离心率相等

    【答案】D
    【解析】解：根据题意，双曲线C1： ﹣y2=1，其焦点在x轴上，c= ， 则其焦点坐标为（ ，0），顶点坐标（a，0），渐近线方程：y=± x，离心率e= ；
    双曲线C2： ﹣x2=1，其焦点在y轴上，c= ，
    则其焦点坐标为（0， ），顶点坐标（0，a），渐近线方程：y=±ax，离心率e= ；
    分析可得：双曲线C1： ﹣y2=1与双曲线C2： ﹣x2=1的离心率相同；
    故选：D．
    根据题意，由双曲线C1与C2的标准方程，分析其焦点位置，进而求出C1与C2的焦点坐标、顶点坐标、渐近线方程以及离心率，比较即可得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某种子培育基地新研发了两种型号的种子，从中选出90粒进行发芽试验，并根据结果对种子进行改良.将试验结果汇总整理绘制成如下列联表：

    （1）将列联表补充完整，并判断是否有99%的把握认为发芽和种子型号有关；

    （2）若按照分层抽样的方式，从不发芽的种子中任意抽取20粒作为研究小样本，并从这20粒研究小样本中任意取出3粒种子，设取出的型号的种子数为，求的分布列与期望.

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    ，其中.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本题满分16分）某批发公司批发某商品，每件商品进价80元，批发价120元，该批发商为鼓励经销商批发，决定当一次批发量超过100个时，每多批发一个，批发的全部商品的单价就降低0．04元，但最低批发价不能低于102元．

    （1）当一次订购量为多少个时,每件商品的实际批发价为102元?

    （2）当一次订购量为个, 每件商品的实际批发价为元,写出函数的表达式；

    （3）根据市场调查发现,经销商一次最大定购量为个，则当经销商一次批发多少个零件时,该批发公司可获得最大利润．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某闯关游戏规则是：先后掷两枚骰子，将此试验重复n轮，第n轮的点数分别记为xn ， yn ， 如果点数满足xn＜ ，则认为第n轮闯关成功，否则进行下一轮投掷，直到闯关成功，游戏结束．
    （Ⅰ）求第一轮闯关成功的概率；
    （Ⅱ）如果第i轮闯关成功所获的奖金数f（i）=10000× （单位：元），求某人闯关获得奖金不超过1250元的概率；
    （Ⅲ）如果游戏只进行到第四轮，第四轮后不论游戏成功与否，都终止游戏，记进行的轮数为随机变量X，求x的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列集合中表示同一集合的是( )

    A.，B.，

    C.，D.，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为提高员工的综合素质，聘请专业机构对员工进行专业技术培训，其中培训机构费用成本为12000元.公司每位员工的培训费用按以下方式与该机构结算：若公司参加培训的员工人数不超过30人时，每人的培训费用为850元；若公司参加培训的员工人数多于30人，则给予优惠：每多一人，培训费减少10元.已知该公司最多有60位员工可参加培训，设参加培训的员工人数为人，每位员工的培训费为元，培训机构的利润为元.

    （1）写出与 之间的函数关系式；

    （2）当公司参加培训的员工为多少人时，培训机构可获得最大利润？并求最大利润.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二项式展开式中各项系数之和比各二项式系数之和大240，

    (1)求；(2)求展开式中含项的系数；(3)求展开式中所有含的有理项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某学校准备修建一个面积为2400平方米的矩形活动场地（图中ABCD）的围栏，按照修建要求，中间用围墙EF隔开，使得ABEF为矩形，EFCD为正方形，设米，已知围墙（包括EF）的修建费用均为每米500元，设围墙（包括EF）的修建总费用为y元．

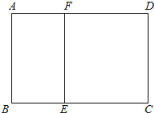
    （1）求出y关于x的函数解析式及x的取值范围；

    （2）当x为何值时，围墙（包括EF）的修建总费用y最小？并求出y的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面直角坐标系xOy中，以O为极点，x轴的非负半轴为极轴建立极坐标系，P点的极坐标为（3， ）．曲线C的参数方程为ρ=2cos（θ﹣ ）（θ为参数）．
    （Ⅰ）写出点P的直角坐标及曲线C的直角坐标方程；
    （Ⅱ）若Q为曲线C上的动点，求PQ的中点M到直线l：2ρcosθ+4ρsinθ= 的距离的最小值．

    查看答案和解析>>

    同步练习册答案