
【题目】设函数![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() 存在三个极值点
存在三个极值点![]() ,且
,且![]() ,求
,求![]() 的取值范围,并证明:
的取值范围,并证明:![]() .
.
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 的图像是一条连续不断的曲线,且在任意区间上
的图像是一条连续不断的曲线,且在任意区间上![]() 都不是常值函数.设
都不是常值函数.设![]() ,其中分点
,其中分点![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间
个小区间![]() ,记
,记![]() ,称为
,称为![]() 关于区间
关于区间![]() 的
的![]() 阶划分“落差总和”.
阶划分“落差总和”.
当![]() 取得最大值且
取得最大值且![]() 取得最小值
取得最小值![]() 时,称
时,称![]() 存在“最佳划分”
存在“最佳划分”![]() .
.
(1)已知![]() ,求
,求![]() 的最大值
的最大值![]() ;
;
(2)已知![]() ,求证:
,求证:![]() 在
在![]() 上存在“最佳划分”
上存在“最佳划分”![]() 的充要条件是
的充要条件是![]() 在
在![]() 上单调递增.
上单调递增.
(3)若![]() 是偶函数且存在“最佳划分”
是偶函数且存在“最佳划分”![]() ,求证:
,求证:![]() 是偶数,且
是偶数,且![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 ,(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为(ρ﹣2cosθ)2=5﹣4sin2θ.
,(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为(ρ﹣2cosθ)2=5﹣4sin2θ.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相切,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)的一种,现有十二生肖的吉祥物各一个,甲、乙、丙三位同学依次选一个作为礼物,甲同学喜欢牛、马和羊,乙同学喜欢牛、兔、狗和羊,丙同学哪个吉祥物都喜欢,则让三位同学选取的礼物都满意的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“公平正义”是社会主义和谐社会的重要特征,是社会主义法治理念的价值追求.“考试”作为一种公平公正选拔人才的有效途径,正被广泛采用.每次考试过后,考生最关心的问题是:自己的考试名次是多少?自已能否被录取?能获得什么样的职位?
某单位准备通过考试(按照高分优先录取的原则)录用![]() 名,其中
名,其中![]() 个高薪职位和
个高薪职位和![]() 个普薪职位.实际报名人数为
个普薪职位.实际报名人数为![]() 名,考试满分为
名,考试满分为![]() 分. 考试后对部分考生考试成绩进行抽样分析,得到频率分布直方图如下:
分. 考试后对部分考生考试成绩进行抽样分析,得到频率分布直方图如下:
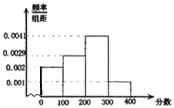
试结合此频率分布直方图估计:
(1)此次考试的中位数是多少分(保留为整数)?
(2)若考生甲的成绩为280分,能否被录取?若能被录取,能否获得高薪职位?(分数精确到个位,概率精确到千分位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在矩形![]() 中,
中,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 折起到
折起到![]() (
(![]() 平面
平面![]() )的位置,
)的位置,![]() 为线段
为线段![]() 的中点.
的中点.
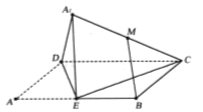
(1)求证:![]() 平面
平面![]() ;
;
(2)已知![]() ,当平面
,当平面![]() 平面
平面![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且原点到直线
,且原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切.试探究
相切.试探究![]() 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,x轴的非负半轴为极轴建立极坐标系,并在两种坐标系中取相同的长度单位已知直线l的参数方程为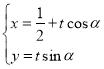 (
(![]() 为参数,
为参数,![]() ),抛物线C的普通方程为
),抛物线C的普通方程为![]() .
.
(1)求抛物线C的准线的极坐标方程;
(2)设直线l与抛物线C相交于A,B两点,求![]() 的最小值及此时
的最小值及此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com