
【题目】已知函数![]() .
.
(1)求函数![]() 的值域;
的值域;
(2)设![]() ,
, ![]() ,
, ![]() ,求函数
,求函数![]() 的最小值
的最小值![]() ;
;
(3)对(2)中的![]() ,若不等式
,若不等式![]() 对于任意的
对于任意的![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ; (2)
; (2) 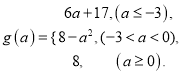 ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)利用函数单调性得证明方法证明函数在![]() 上是增函数,利用单调性求其值域;(2)通过换元法,问题转化为二次函数求最小值,利用对称轴分类讨论即可;(3)分离参数,求函数的最值,求最值时利用函数单调性.
上是增函数,利用单调性求其值域;(2)通过换元法,问题转化为二次函数求最小值,利用对称轴分类讨论即可;(3)分离参数,求函数的最值,求最值时利用函数单调性.
试题解析:(1) 在![]() 任取
任取![]() 且
且![]() ,则
,则![]() ,
, ![]() ,
,
所以, 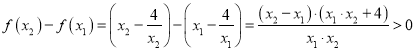 ,即
,即![]() ,
,
所以![]() 是
是![]() 上增函数,故当
上增函数,故当![]() 时,
时, ![]() 取得最小值
取得最小值![]() ,当
,当![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,所以函数
,所以函数![]() 的值域为
的值域为![]() .
.
(2) ![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,则
,则.
①当![]() 时,
时, ![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ;
;
②当![]() 时,
时, ![]() 在
在![]() 上单调递减,故
上单调递减,故![]() ;
;
③当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故
上单调递增,故![]() ;
;
综上所述, 
(3)由(2)知,当![]() 时,
时, ![]() ,所以
,所以![]() ,
,
即![]() ,整理得,
,整理得, ![]() .
.
因为![]() ,所以
,所以![]() 对于任意的
对于任意的![]() 时恒成立.
时恒成立.
令![]() ,
, ![]() ,问题转化为
,问题转化为![]() .
.
在![]() 任取
任取![]() 且
且![]() ,则
,则![]() ,
, ![]() ,
,
所以,  ,
,
①当![]() 时,
时, ![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,
时, ![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以函数![]() 在
在![]() 上单调递减;
上单调递减;
综上, ![]() ,从而
,从而![]() .
.
所以,实数![]() 的取值范围是
的取值范围是![]() .
.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人用农药治虫,由于计算错误,在A,B两个喷雾器中分别配制成12%和6%的药水各10千克,实际要求两个喷雾器中的农药的浓度是一样的,现在只有两个能容纳1千克药水的药瓶,他们从A,B两个喷雾器中分别取1千克的药水,将A中取得的倒入B中,B中取得的倒入A中,这样操作进行了n次后,A喷雾器中药水的浓度为an%,B喷雾器中药水的浓度为bn%.
(1)证明an+bn是一个常数;
(2)求an与an-1的关系式;
(3)求an的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司决定每月给推销员确定个具体的销售目标,对推销员实行目标管理.销售目标确定的适当与否,直接影响公司的经济效益和推销员的工作积极性,为此,该公司当月随机抽取了50位推销员上个月的月销售额(单位:万元),绘制成如图所示的频率分布直方图.

(1)①根据图中数据,求出月销售额在![]() 小组内的频率.
小组内的频率.
②根据直方图估计,月销售目标定为多少万元时,能够使70%的推销员完成任务?并说明理由.
(2)该公司决定从月销售额为![]() 和
和![]() 的两个小组中,选取2位推销员介绍销售经验,求选出的推销员来自同一个小组的概率.
的两个小组中,选取2位推销员介绍销售经验,求选出的推销员来自同一个小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人的卷舌与平舌(指是否能左右卷起来)同人的眼皮单双一样,也是由遗传自父母的基因决定的,其中显性基因记作D,隐性基因记作d;成对的基因中,只要出现了显性基因,就一定是卷舌的(这就是说,“卷舌”的充要条件是“基因对是![]() ,
,![]() 或
或![]() ”).同前面一样,决定眼皮单双的基因仍记作B(显性基因)和b(隐性基因).
”).同前面一样,决定眼皮单双的基因仍记作B(显性基因)和b(隐性基因).
有一对夫妻,两人决定舌头形态和眼皮单双的基因都是![]() ,不考虑基因突变,求他们的孩子是卷舌且单眼皮的概率.(有关生物学知识表明:控制上述两种不同性状的基因遗传时互不干扰).
,不考虑基因突变,求他们的孩子是卷舌且单眼皮的概率.(有关生物学知识表明:控制上述两种不同性状的基因遗传时互不干扰).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型水果超市每天以![]() 元/千克的价格从水果基地购进若干
元/千克的价格从水果基地购进若干![]() 水果,然后以
水果,然后以![]() 元/千克的价格出售,若有剩余,则将剩下的水果以
元/千克的价格出售,若有剩余,则将剩下的水果以![]() 元/千克的价格退回水果基地,为了确定进货数量,该超市记录了
元/千克的价格退回水果基地,为了确定进货数量,该超市记录了![]() 水果最近
水果最近![]() 天的日需求量(单位:千克),整理得下表:
天的日需求量(单位:千克),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天记录的各日需求量的频率代替各日需求量的概率.
天记录的各日需求量的频率代替各日需求量的概率.
(1)求该超市![]() 水果日需求量
水果日需求量![]() (单位:千克)的分布列;
(单位:千克)的分布列;
(2)若该超市一天购进![]() 水果
水果![]() 千克,记超市当天
千克,记超市当天![]() 水果获得的利润为
水果获得的利润为![]() (单位:元),求
(单位:元),求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]()
![]() ,过直线
,过直线![]() :
:![]() 上任一点
上任一点![]() 向抛物线
向抛物线![]() 引两条切线
引两条切线![]() (切点为
(切点为![]() ,且点
,且点![]() 在
在![]() 轴上方).
轴上方).
(1)求证:直线![]() 过定点,并求出该定点;
过定点,并求出该定点;
(2)抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面α及直线a,b,则下列说法正确的是( )
A. 若直线a,b与平面α所成角都是30°,则这两条直线平行
B. 若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直
C. 若直线a,b平行,则这两条直线中至少有一条与平面α平行
D. 若直线a,b垂直,则这两条直线与平面α不可能都垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:![]() 与
与![]() 轴负半轴的交点为A,点P在直线l:
轴负半轴的交点为A,点P在直线l:![]() 上,过点P作圆O的切线,切点为T.
上,过点P作圆O的切线,切点为T.
(1)若a=8,切点![]() ,求直线AP的方程;
,求直线AP的方程;
(2)若PA=2PT,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com