
����Ŀ���������з��ز�������ʾ����������ǰ5�����½�סլ���۾�������������Ϊ���Ʒ��۹������ǣ�������6�·ݿ�ʼ�Ƴ��۷��Ⱥ�۵��ش�ʩ��6�·ݿ�ʼ���۵õ��ܺõ����ƣ����ۻ��䣮����ǰ10���µķ��۾��������
�·�x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
����y����Ԫ/ƽ���ף� | 0.83 | 0.95 | 1.00 | 1.05 | 1.17 | 1.15 | 1.10 | 1.06 | 0.98 | 0.94 |
�ز������о����֣���1�·���5�·ݵĸ��¾���y����Ԫ/ƽ���ף���x֮�������������ع�ϵ����6�·���10�·ݵĸ��¾���y����Ԫ/ƽ���ף���x֮����и�������ع�ϵ��
��1�������������أ�����ǰ5���µ����ݣ���y����x�Ļع�ֱ�߷��̣���Ԥ��12�·ݵķ��ز����ۣ�����ȷ��0.01��
��2���������غ�6�·���10�·ݵ����ݿɵõ�y��x�Ļع�ֱ�߷���Ϊ��![]() ���ɴ�Ԥ���������غ�12�·ݵķ��ز����ۣ�˵���������صı�Ҫ�ԣ�����ȷ��0.01��
���ɴ�Ԥ���������غ�12�·ݵķ��ز����ۣ�˵���������صı�Ҫ�ԣ�����ȷ��0.01��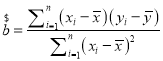 ��
��![]() ��
��
���𰸡���1��![]() 0.078x+0.766��ÿƽ����1.7��Ԫ����2��0.83��Ԫÿƽ���ף�������
0.078x+0.766��ÿƽ����1.7��Ԫ����2��0.83��Ԫÿƽ���ף�������
��������
��1����![]() �·ݵ���Ϣ������ع�ϵ���Ĺ�ʽ���ɵõ��ع鷽�̣��ٽ�
�·ݵ���Ϣ������ع�ϵ���Ĺ�ʽ���ɵõ��ع鷽�̣��ٽ�![]() ����
����![]() ���ɵõ�
���ɵõ�![]() �·ݵ��½����ز��ļ۸�
�·ݵ��½����ز��ļ۸�
��2����![]() ����
����![]() ���õ��غ�Ļع鷽�̵õ�
���õ��غ�Ļع鷽�̵õ�![]() �·ݵ��½����ز��۸���(1)�е����ݱȽϼ��ɿ������ص�Ч��.
�·ݵ��½����ز��۸���(1)�е����ݱȽϼ��ɿ������ص�Ч��.
��1��![]() 3��
3��
![]() 1��
1��
![]()
![]() 0.78��
0.78��
![]() ��
��
��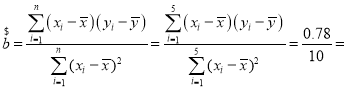 0.078��
0.078��
![]() 1��0.078��3��0.766��
1��0.078��3��0.766��
��y����x�Ļع�ֱ�߷���Ϊ��![]() 0.078x+0.766��
0.078x+0.766��
![]() ���뷽�̵ã�
���뷽�̵ã�![]() 1.70����Ԫ��
1.70����Ԫ��
���������������أ�Ԥ��12�·ݵ��½����ز����۽��ﵽÿƽ����1.7��Ԫ��
��2���������غ�6�·���10�·ݵ����ݣ�
![]() ��
��
![]() ��
��
![]()
![]() ��
��
![]() ��
��
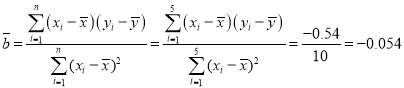 ��
��
![]()
�õ�y������Ļع鷽��Ϊ��![]() 0.054x+1.48��
0.054x+1.48��
�൱![]() ʱ��
ʱ��![]() 0.054��12+1.48��0.83����Ԫ����
0.054��12+1.48��0.83����Ԫ����
���������غ�Ԥ�Ƶ�12�·ݵ��½����ز����۽����䵽0.83��Ԫÿƽ���ף��Կ��Ʒ��۹�����������������Ч������̨����Ч���Ƿdz��б�Ҫ�ģ�


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����alnx![]() 1��g��x����x3
1��g��x����x3![]() 3tx+1��t��0����
3tx+1��t��0����
��1����a![]() ʱ����f��x��������[
ʱ����f��x��������[![]() ��e]�ϵ���ֵ��
��e]�ϵ���ֵ��
��2�����ۺ���f��x���ĵ����ԣ�
��3����g��x����xex��m+2��eΪ��Ȼ�����ĵ�����������x��[0��+���������ʱm�����ֵΪ1����t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����|2x+1|��2|x��m|��m��N����f��x����3�����.
��1����m��ֵ��
��2����![]() ��
��![]() ʱ��f��a��+f��b������2��֤����
ʱ��f��a��+f��b������2��֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ����
����![]() ��
��![]() ��ͼ����һ��б��Ϊ1�Ĺ����ߣ�
��ͼ����һ��б��Ϊ1�Ĺ����ߣ�![]() Ϊ��Ȼ�����ĵ�����.
Ϊ��Ȼ�����ĵ�����.
��1����![]() ��
��
��2���躯��![]() �����ۺ���
�����ۺ���![]() ��������.
��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��ֱ������
��ֱ������![]() ��϶��ɵļ������У��ı���
��϶��ɵļ������У��ı���![]() �����Σ�
������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() Ϊ
Ϊ![]() ���е�.
���е�.

��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2������![]() ���߶�
���߶�![]() �ϣ������˵㣩���������
�ϣ������˵㣩���������![]() ������ֵΪ
������ֵΪ![]() ����
����![]() �ij���.
�ij���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������(semiregular solid) ����������¶������������ɱ�����ȫ��ͬ���������Ϊ��Ķ����壬��������ѧ�ĶԳ�������ʮ�ĵȱ������һ�ְ��������壬�����������нض��ɵģ����ɰ˸��������κ�����������Ϊ��İ���������.��ͼ��ʾ��ͼ�������DZ߳�Ϊ1�������Σ����߲�����ij��ʮ�ĵȱ��������ͼ����ü���������Ϊ�� ��
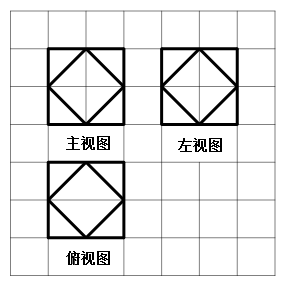
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ⳤΪa��������ABCD��A1B1C1D1�У�P��Q��L�ֱ�Ϊ��A1D1��C1D1��BC���е㣮
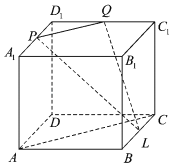
��1����֤��AC��QL��
��2����������DPQL�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ĵ���
�ĵ���![]() ��ֱ�����Σ�
��ֱ�����Σ�![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() .
.
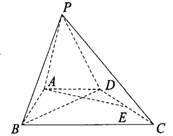
��1��֤��:ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��ƽ��
��ƽ��![]() ���ɵĽ�Ϊ
���ɵĽ�Ϊ![]() ��������
��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ![]() (
(![]() )��һ������
)��һ������![]() ��
��![]() Ϊ��Բ
Ϊ��Բ![]() ��һ��,����Բ
��һ��,����Բ![]() �ϴ���һ��
�ϴ���һ��![]() ��ʹ��
��ʹ��![]() ������Բ
������Բ![]() �������ʵ�ȡֵ��Χ�ǣ� ��
�������ʵ�ȡֵ��Χ�ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com