
(A)若不等式|x+1|-|x―4|≥a+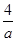 ,对任意的x∈R恒成立,则实数a的取值范围是
,对任意的x∈R恒成立,则实数a的取值范围是
(B)已知直线l∶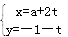 (t为参数),圆C∶r=2
(t为参数),圆C∶r=2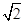 cos(q―
cos(q―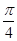 )(极轴与x轴的非负半轴重合,且单位长度相同),若直线l被圆C截得弦长为2,则a=
)(极轴与x轴的非负半轴重合,且单位长度相同),若直线l被圆C截得弦长为2,则a=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com