
【题目】已知等差数列{an}的前n项和为Sn , 且a2=﹣5,S5=﹣20.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求使不等式Sn>an成立的n的最小值.
【答案】解:(Ⅰ)设{an}的公差为d,
依题意,有a2=a1+d=﹣5,S5=5a1+10d=﹣20,
联立得 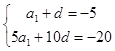
解得 ![]() ,
,
所以an=﹣6+(n﹣1)1=n﹣7.
(Ⅱ)因为an=n﹣7,
所以 ![]() ,
,
令 ![]() ,
,
即n2﹣15n+14>0,
解得n<1或n>14,
又n∈N* , 所以n>14,
所以n的最小值为15
【解析】(Ⅰ)设{an}的公差为d,利用首项a1及公差d表示已知,解方程即可求解a1 , d,进而可求通项公式.(Ⅱ)利用等差数列的求和公式及通项公式代入已知,整理解不等式即可求解n的范围,可求.
【考点精析】本题主要考查了等差数列的前n项和公式的相关知识点,需要掌握前n项和公式:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a. 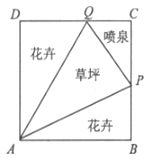
(1)当∠PAQ= ![]() 时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
(2)考虑到小区道路的整体规划,要求PB+DQ=PQ,请探究∠PAQ是否为定值,若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,我国南海某处的一个圆形海域上有四个小岛,小岛B与小岛A、小岛C相距都为5n mile,与小岛D相距为 ![]() n mile.小岛A对小岛B与D的视角为钝角,且
n mile.小岛A对小岛B与D的视角为钝角,且 ![]() .
.
(Ⅰ)求小岛A与小岛D之间的距离和四个小岛所形成的四边形的面积;
(Ⅱ)记小岛D对小岛B与C的视角为α,小岛B对小岛C与D的视角为β,求sin(2α+β)的值.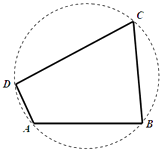
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆![]() 的极坐标方程为
的极坐标方程为![]() ,若以极点
,若以极点![]() 为原点,极轴所在的直线为
为原点,极轴所在的直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求圆![]() 的参数方程;
的参数方程;
(2)在直线坐标系中,点![]() 是圆
是圆![]() 上的动点,试求
上的动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲正弦函数shx= ![]() 和双曲余弦函数chx=
和双曲余弦函数chx= ![]() 与我们学过的正弦函数和余弦函数有许多类似的性质,请类比正弦函数和余弦函数的和角公式,写出双曲正弦或双曲余弦函数的一个类似的正确结论 .
与我们学过的正弦函数和余弦函数有许多类似的性质,请类比正弦函数和余弦函数的和角公式,写出双曲正弦或双曲余弦函数的一个类似的正确结论 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知长方体ABCD﹣A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C.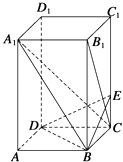
(1)求CE的长;
(2)求证:A1C⊥平面BED;
(3)求A1B与平面BDE夹角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下命题中,正确命题的序号是 . ①函数y=tanx在定义域内是增函数;
②函数y=2sin(2x+ ![]() )的图象关于x=
)的图象关于x= ![]() 成轴对称;
成轴对称;
③已知 ![]() =(3,4),
=(3,4), ![]()
![]() =﹣2,则向量
=﹣2,则向量 ![]() 在向量
在向量 ![]() 的方向上的投影是﹣
的方向上的投影是﹣ ![]()
④如果函数f(x)=ax2﹣2x﹣3在区间(﹣∞,4)上是单调递减的,则实数a的取值范围是(0, ![]() ].
].
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是由
是由![]() 个有序实数构成的一个数组,记作
个有序实数构成的一个数组,记作![]() ,其中
,其中![]()
![]()
![]() 称为数组
称为数组![]() 的“元”,
的“元”, ![]() 称为
称为![]() 的下标,如果数组
的下标,如果数组![]() 中的每个“元”都是来自数组
中的每个“元”都是来自数组
![]() 中不同下标的“元”,则称
中不同下标的“元”,则称![]() 为
为![]() 的子数组,定义两个数组
的子数组,定义两个数组![]() 和
和![]()
![]() 的关系数为
的关系数为![]() ;
;
(1)若![]() ,
, ![]() ,设
,设![]() 是
是![]() 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求![]()
的最大值;
(2)若 ,
, ![]() ,且
,且![]() ,
, ![]() 为
为![]() 的含有三个“元”
的含有三个“元”
的子数组,求![]() 的最大值;
的最大值;
(3)若数组![]() 中的“元”满足
中的“元”满足![]() ,设数组
,设数组![]()
![]() 含有
含有
四个“元”![]() ,且
,且![]() ,求
,求![]() 与
与![]() 的所有含有三个“元”
的所有含有三个“元”
的子数组的关系数的最大值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com