
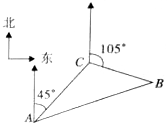
 如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时.
如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时. 分析 设所需时间为t小时,在点B处相遇则可求得AB和BC,进而利用余弦定理建立等式求得t.
解答 解:设所需时间为t小时,在点B处相遇在△ABC中,
∠ACB=120°,AC=100,AB=21t,BC=9t,由余弦定理:
(21t)2=102+(9t)2-2×10×9t×cos120°
整理得:36t2-9t-10=0
解得:t=$\frac{2}{3}$或-$\frac{5}{12}$(舍负)
故救生艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$.
故答案为$\frac{2}{3}$.
点评 本题主要考查了解三角形的实际应用.解题的关键是利用了余弦定理,利用已知的边和角建立方程求得时间.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{4}{3}}]$ | B. | $({-∞,\frac{3}{4}})$ | C. | $[{-\frac{3}{4},+∞})$ | D. | $[{-\frac{4}{3},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | $\frac{24}{5}$ | D. | $\frac{36}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{4}$,0) | B. | ($-\frac{1}{2}$,-$\frac{1}{4}$) | C. | ($-\frac{1}{2}$,$-\frac{1}{4}$)∪($-\frac{1}{4}$,-$\frac{1}{8}$) | D. | (-$\frac{1}{2}$,$-\frac{1}{8}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com