
【题目】在直角坐标系xOy中,直线l的参数方程为![]() (t为参数),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ(ρ﹣2sinθ)=1.
(t为参数),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ(ρ﹣2sinθ)=1.
(1)求C的直角坐标方程;
(2)设直线l与y轴相交于P,与曲线C相交于A、B两点,且|PA|+|PB|=2,求点O到直线l的距离.
【答案】(1)x2+(y﹣1)2=2(2)![]()
【解析】
(1)把曲线C的极坐标方程变形,结合ρ2=x2+y2,x=ρcosθ,y=ρsinθ可得C的直角坐标方程;
(2)直线l与y轴的交点为P(0,﹣1),曲线C是圆心为C(0,1),半径为![]() 的圆,由CP=2可得P(0,﹣1)在圆外,将直线l的参数方程
的圆,由CP=2可得P(0,﹣1)在圆外,将直线l的参数方程![]() 代入x2+(y﹣1)2=2,得到关于t的一元二次方程,利用根与系数的关系及参数t的几何意义求解.
代入x2+(y﹣1)2=2,得到关于t的一元二次方程,利用根与系数的关系及参数t的几何意义求解.
(1)∵曲线C的极坐标方程为ρ(ρ﹣2sinθ)=1,
化简得:ρ2﹣2ρcosθ﹣1=0,
由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,
得C的直角坐标方程为x2+y2﹣2y﹣1=0,即x2+(y﹣1)2=2;
(2)直线l与y轴的交点为P(0,﹣1),曲线C是圆心为C(0,1),半径为![]() 的圆,
的圆,
∵CP=2,∴P(0,﹣1)在圆外,
将直线l的参数方程![]() 代入x2+(y﹣1)2=2,
代入x2+(y﹣1)2=2,
得t2﹣4tsinα+2=0.
∴t1+t2=4sinα,又P(0,﹣1)在圆外,
∴t1,t2同号,
∴|PA|+|PB|=|t1|+|t2|=|t1+t2|=|4sinα|=2,
得|sinα|![]() ,可得直线l的斜率为
,可得直线l的斜率为![]() .
.
设点O到直线l的距离为h,则h=|OP|sin60°![]() .
.
即点O到直线l的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】某调查机构为了解人们对某个产品的使用情况是否与性别有关,在网上进行了问卷调查,在调查结果中随机抽取了![]() 份进行统计,得到如下
份进行统计,得到如下![]() 列联表:
列联表:
男性 | 女性 | 合计 | |
使用 | 15 | 5 | 20 |
不使用 | 10 | 20 | 30 |
合计 | 25 | 25 | 50 |
(1)请根据调查结果你有多大把握认为使用该产品与性别有关;
(2)在不使用该产品的人中,按性别用分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人参加某项活动,记被抽中参加该项活动的女性人数为
人参加某项活动,记被抽中参加该项活动的女性人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: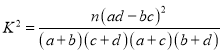 ,
,
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=2an﹣1.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=anlog2an+1,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是![]() ,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C经过伸缩变换
,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C经过伸缩变换 得到曲线E,直线l:
得到曲线E,直线l: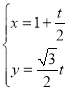 (t为参数)与曲线E交于A,B两点,
(t为参数)与曲线E交于A,B两点,
(1)设曲线C上任一点为![]() ,求
,求![]() 的最小值;
的最小值;
(2)求出曲线E的直角坐标方程,并求出直线l被曲线E截得的弦AB长;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com