
【题目】某校高三共有800名学生,为了解学生3月月考生物测试情况,根据男女学生人数差异较大,从中随机抽取了200名学生,记录他们的分数,并整理得如图频率分布直方图.
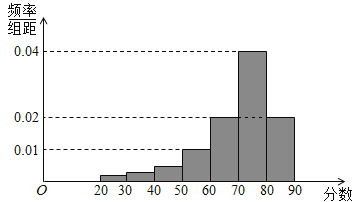
(1)若成绩不低于60分的为及格,成绩不低于80分的为优秀,试估计总体中合格的有多少人?优秀的有多少人?
(2)已知样本中有一半的女生分数不小于80,且样本中不低于80分的男女生人数之比2:3,试估计总体中男生和女生人数的比例.
【答案】(1)及格的有640人,优秀的有160人.(2)![]()
【解析】试题分析:(1)根据频率分布直方图得到成绩及格和成绩优秀的频率,根据“频数=频率×样本容量”得的人数;(2)根据频率分布直方图得到样本中不低于80分的女生人数为40人,所以样本中分数不小于80的女生人数为![]() ,从而得到样本中的女生人数为
,从而得到样本中的女生人数为![]() ,男生人数为
,男生人数为![]() ,然后根据分层抽样的原理可得男生和女生人数的估计比例。
,然后根据分层抽样的原理可得男生和女生人数的估计比例。
试题解析:
(1)根据频率分布直方图可知,
总体中及格的人数估计为![]() ,
,
总体中优秀的人数估计为![]() ,
,
所以估计总体中及格的有640人,优秀的有160人.
(2)由题意可知,样本中分数不小于80的学生人数为![]() ,
,
所以样本中分数不小于80的女生人数为![]() ,
,
所以样本中的女生人数为![]() ,男生人数为
,男生人数为![]() ,
,
男生和女生人数的比例为![]() ,
,
所以根据分层抽样原理,总体中男生和女生人数的比例估计为![]() .
.


科目:高中数学 来源: 题型:
【题目】某港口船舶停靠的方案是先到先停.
(1)若甲乙两艘船同时到达港口,双方约定各派一名代表猜拳:从1,2,3,4,5中各随机选一个数,若两数之和为偶数,则甲先停靠;若两数之和为奇数,则乙先停靠,这种规则是否公平?请说明理由.
(2)根据以往经验,甲船将于早上![]() 到达,乙船将于早上
到达,乙船将于早上![]() 到达,请应用随机模拟的方法求甲船先停靠的概率,随机数模拟实验数据参考如下:记
到达,请应用随机模拟的方法求甲船先停靠的概率,随机数模拟实验数据参考如下:记![]() ,
, ![]() 都是
都是![]() 之间的均匀随机数,用计算机做了100次试验,得到的结果有12次满足
之间的均匀随机数,用计算机做了100次试验,得到的结果有12次满足![]() ,有6次满足
,有6次满足![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() :
: ![]() 上,与直线
上,与直线![]() :
: ![]() 相切,且截直线
相切,且截直线![]() :
: ![]() 所得弦长为6
所得弦长为6
(Ⅰ)求圆![]() 的方程
的方程
(Ⅱ)过点![]() 是否存在直线
是否存在直线![]() ,使以
,使以![]() 被圆
被圆![]() 截得弦
截得弦![]() 为直径的圆经过原点?若存在,写出直线的方程;若不存在,说明理由.
为直径的圆经过原点?若存在,写出直线的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)求函数![]() 的对称轴方程;
的对称轴方程;
(II)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() 分别是△ABC三个内角A,B,C的对边,a=2,c=4,且
分别是△ABC三个内角A,B,C的对边,a=2,c=4,且![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)求函数![]() 的对称轴方程;
的对称轴方程;
(II)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() 分别是△ABC三个内角A,B,C的对边,a=2,c=4,且
分别是△ABC三个内角A,B,C的对边,a=2,c=4,且![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的解析式满足 ![]() .
.
(1)求函数f(x)的解析式;
(2)当a=1时,试判断函数f(x)在区间(0,+∞)上的单调性,并加以证明;
(3)当a=1时,记函数 ![]() ,求函数g(x)在区间
,求函数g(x)在区间 ![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分层抽样是将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法;在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱多少衰出之,问各几何?”其译文为:今有甲持560钱,乙持350钱,丙持180钱,甲、乙、丙三人一起出关,关税共100钱,要按照各人带钱多少的比例进行交税,问三人各应付多少税?则下列说法错误的是( )
A. 甲应付![]() 钱 B. 乙应付
钱 B. 乙应付![]() 钱
钱
C. 丙应付![]() 钱 D. 三者中甲付的钱最多,丙付的钱最少
钱 D. 三者中甲付的钱最多,丙付的钱最少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)是否存在实数![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调研学生在![]() ,
, ![]() 两家餐厅用餐的满意度,从在
两家餐厅用餐的满意度,从在![]() ,
, ![]() 两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以10为组距分成6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到
,得到![]() 餐厅分数的频率分布直方图,和
餐厅分数的频率分布直方图,和![]() 餐厅分数的频数分布表:
餐厅分数的频数分布表:
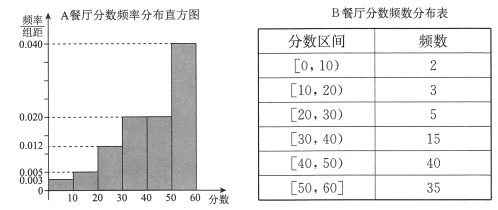
(Ⅰ)在抽样的100人中,求对![]() 餐厅评分低于30的人数;
餐厅评分低于30的人数;
(Ⅱ)从对![]() 餐厅评分在
餐厅评分在![]() 范围内的人中随机选出2人,求2人中恰有1人评分在
范围内的人中随机选出2人,求2人中恰有1人评分在![]() 范围内的概率;
范围内的概率;
(Ⅲ)如果从![]() ,
, ![]() 两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com