
【题目】已知动直线l与椭圆C:![]() 交于
交于![]() ,
,![]() 两个不同的点,O为坐标原点.
两个不同的点,O为坐标原点.
![]() 若直线l过点
若直线l过点![]() ,且原点到直线l的距离为
,且原点到直线l的距离为![]() ,求直线l的方程;
,求直线l的方程;
![]() 若
若![]() 的面积
的面积![]() ,求证:
,求证:![]() 和
和![]() 均为定值;
均为定值;
![]() 椭圆C上是否存在三点D、E、G,使得
椭圆C上是否存在三点D、E、G,使得![]() ?若存在,判断
?若存在,判断![]() 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由.
【答案】(1)![]() 见解析;(3)见解析
见解析;(3)见解析
【解析】
![]() 先设直线方程为
先设直线方程为![]() ,根据原点到直线l的距离为
,根据原点到直线l的距离为![]() ,列出方程即可求出
,列出方程即可求出![]() ,进而可得出结果;
,进而可得出结果;
![]() 分直线斜率存在和不存在两种情况讨论,联立直线与椭圆方程,结合韦达定理等即可证明结论成立;
分直线斜率存在和不存在两种情况讨论,联立直线与椭圆方程,结合韦达定理等即可证明结论成立;
![]() 先假设存在
先假设存在![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,结合(2)中的结果推出矛盾即可.
,结合(2)中的结果推出矛盾即可.
![]() 设直线方程为
设直线方程为![]() ,
,![]() 原点到直线l的距离为
原点到直线l的距离为![]() ,
,![]() ,
,
解得![]() 时,此时直线方程为
时,此时直线方程为![]() ,
,
![]() 当直线l的斜率不存在时,P,Q两点关于x轴对称,
当直线l的斜率不存在时,P,Q两点关于x轴对称,
所以![]() ,
,![]() ,
,![]() 在椭圆上,
在椭圆上,![]()
又![]() ,
,![]()
由![]() 得
得![]() ,
,![]() 此时
此时![]() ,
,![]() ;
;
![]() 当直线l的斜率存在时,是直线l的方程为
当直线l的斜率存在时,是直线l的方程为![]() ,将其代入
,将其代入![]() 得
得
![]() ,
,![]()
即![]() ,又
,又![]() ,
,![]() ,
,
![]() ,
,
![]() 点O到直线l的距离为
点O到直线l的距离为![]() ,
,
![]()
又![]() ,即
,即![]()
整理得![]() ,
,
此时![]() ,
,
![]() ;
;
综上所述![]() ,
,![]() 结论成立.
结论成立.
![]() 椭圆C上不存在三点D,E,G,使得
椭圆C上不存在三点D,E,G,使得![]() ,
,
证明:假设存在![]() ,
,![]() ,
,![]() ,使得
,使得![]()
由![]() 得
得![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]()
解得![]() ;
;![]() .
.
因此u,![]() ,
,![]() 只能从
只能从![]() 中选取,
中选取,
v,![]() ,
,![]() 只能从
只能从![]() 中选取,
中选取,
因此点D,E,G,只能在![]() 这四点中选取三个不同点,
这四点中选取三个不同点,
而这三点的两两连线中必有一条过原点,与![]() 矛盾.
矛盾.
所以椭圆C上不存在满足条件的三点D,E,G.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充,已知金字塔的每一条棱和边都相等.
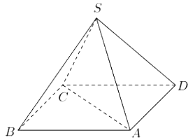
(1)求证:直线AC垂直于直线SD;
(2)若搭边框共使用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电子阅读的普及,传统纸质媒体遭受到了强烈的冲击.某杂志社近9年来的纸质广告收入如表所示:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
广告收入y(千万元) | 2 | 2.2 | 2.5 | 2.8 | 3 | 2.5 | 2.3 | 2 | 1.8 |
根据这9年的数据,对t和y作线性相关性检验,求得样本相关系数的绝对值为0.243;根据后5年的数据,对t和y作线性相关性检验,求得样本相关系数的绝对值为0.984.
(Ⅰ)如果要用线性回归方程预测该杂志社2019年的纸质广告收入,现在有两个方案,
方案一:选取这9年数据进行预测;方案二:选取后5年数据进行预测.
从实际生活背景以及线性相关性检验的角度分析,你觉得哪个方案更合适?
附:
相关性检验的临界值表:
n-2 | 小概率 | |
0.05 | 0.01 | |
3 | 0.878 | 0.959 |
7 | 0.666 | 0.798 |
(Ⅱ)某购物网站同时销售某本畅销书籍的纸质版本和电子书,某班级有五名同学在该网站购买了这本书,其中三人只购买了电子书,另两人只购买了纸质书,从这五人中任取两人,求两人都购买了电子书的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的各项都不为零,其前n项和为
的各项都不为零,其前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 满足
满足![]() ,其中t为正整数.
,其中t为正整数.
![]() 求
求![]() ;
;
![]() 若不等式
若不等式![]() 对任意
对任意![]() 都成立,求首项
都成立,求首项![]() 的取值范围;
的取值范围;
![]() 若首项
若首项![]() 是正整数,则数列
是正整数,则数列![]() 中的任意一项是否总可以表示为数列
中的任意一项是否总可以表示为数列![]() 中的其他两项之积?若是,请给出一种表示方式;若不是,请说明理由.
中的其他两项之积?若是,请给出一种表示方式;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
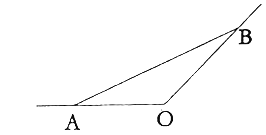
【题目】如图所示,某城市有一条从正西方AO通过市中心O后向东北OB的公路,现要修一条地铁L,在OA,OB上各设一站A,B,地铁在AB部分为直线段,现要求市中心O与AB的距离为![]() ,设地铁在AB部分的总长度为
,设地铁在AB部分的总长度为![]() .
.
![]() 按下列要求建立关系式:
按下列要求建立关系式:
![]() 设
设![]() ,将y表示成
,将y表示成![]() 的函数;
的函数;
![]() 设
设![]() ,
,![]() 用m,n表示y.
用m,n表示y.
![]() 把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面ABFE和CDEF是全等的等腰梯形,左右两坡屋面EAD和FBC是全等的三角形.点F在平面ABCD和BC上的射影分别为H,M.已知HM 5 m,BC 10 m,梯形ABFE的面积是△FBC面积的2.2倍.设∠FMH ![]()
![]() .
.
(1)求屋顶面积S关于![]() 的函数关系式;
的函数关系式;
(2)已知上部屋顶造价与屋顶面积成正比,比例系数为k(k为正的常数),下部主体造价与其 高度成正比,比例系数为16 k.现欲造一栋上、下总高度为6 m的别墅,试问:当![]() 为何值时,总造价最低?
为何值时,总造价最低?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组在科学馆的帕斯卡三角仪器前进行探究实验.如图所示,每次使一个实心小球从帕斯卡三角仪器的顶部入口落下,当它在依次碰到每层的菱形挡板时,会等可能地向左或者向右落下,在最底层的7个出口处各放置一个容器接住小球,该小组连续进行200次试验,并统计容器中的小球个数得到柱状图:
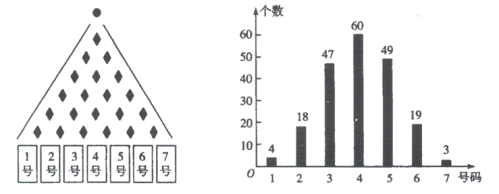
(Ⅰ)用该实验来估测小球落入4号容器的概率,若估测结果的误差小于![]() ,则称该实验是成功的.试问:该兴趣小组进行的实验是否成功?(误差
,则称该实验是成功的.试问:该兴趣小组进行的实验是否成功?(误差![]() )
)
(Ⅱ)再取3个小球进行试验,设其中落入4号容器的小球个数为![]() ,求
,求![]() 的分布列与数学期望.(计算时采用概率的理论值)
的分布列与数学期望.(计算时采用概率的理论值)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com