
【题目】已知函数f(x)=|2x﹣a|+|2x﹣1|(a∈R).
(1)当a=﹣1时,求f(x)≤2的解集;
(2)若f(x)≤|2x+1|的解集包含集合 ![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】
(1)解:a=﹣1时,f(x)=|2x+1|+|2x﹣1|≥|2x+1﹣2x+1|=2,
即x=± ![]() 时,“=”成立,
时,“=”成立,
故不等式的解集是{x|x=± ![]() }
}
(2)解:由|2x﹣a|+|2x﹣1|≤|2x+1|得:|2x﹣a|≤|2x+1|﹣|2x﹣1|≤|2x+1﹣2x﹣1|=2,
故﹣2≤2x﹣a≤2,故 ![]() ≤x≤
≤x≤ ![]() ,
,
故[ ![]() ,1][
,1][ ![]() ,
, ![]() ],
],
故 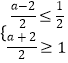 ,解得:a∈[0,3]
,解得:a∈[0,3]
【解析】(1)根据绝对值的选项得到f(x)≥2,求出满足条件的x的值即可;(2)根据绝对值的性质求出x的范围,结合集合的包含关系求出a的范围即可.
【考点精析】通过灵活运用绝对值不等式的解法,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号即可以解答此题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】用部分自然数构造如图的数表:用![]() 表示第
表示第![]() 行第
行第![]() 个数
个数![]() ,使得
,使得![]() ,每行中的其他各数分别等于其“肩膀”上的两个数之和,设第
,每行中的其他各数分别等于其“肩膀”上的两个数之和,设第![]() 行中的各数之和为
行中的各数之和为![]() .
.
已知![]() ,求
,求![]() 的值;
的值;
令![]() ,证明:
,证明:![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
数列![]() 中是否存在不同的三项
中是否存在不同的三项![]() 恰好成等差数列?若存在,求出
恰好成等差数列?若存在,求出![]() 的关系,若不存在,说明理由.
的关系,若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() (
(![]() )的离心率为
)的离心率为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,若椭圆
,若椭圆![]() 与圆
与圆![]() 相交于
相交于![]() ,
, ![]() 两点,且线段
两点,且线段![]() 恰好为圆
恰好为圆![]() 的直径.
的直径.
(1)求直线![]() 的方程;
的方程;
(2)求椭圆![]() 的标准方程.
的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,平面ADNM⊥平面ABCD,四边形ABCD是菱形,ADNM是矩形, ![]() ,AB=2,AM=1,E是AB的中点.
,AB=2,AM=1,E是AB的中点. 
(1)求证:平面DEM⊥平面ABM;
(2)在线段AM上是否存在点P,使二面角P﹣EC﹣D的大小为 ![]() ?若存在,求出AP的长;若不存在,请说明理由.
?若存在,求出AP的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人相约于下午1:00~2:00之间到某车站乘公共汽车外出,他们到达车站的时间是随机的.设在下午1:00~2:00之间该车站有四班公共汽车开出,开车时间分别是1:15,1:30,1:45,2:00.求他们在下述情况下乘同一班车的概率:
(1)约定见车就乘;
(2)约定最多等一班车.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M是满足下列性质的函数![]() 的全体:在定义域内存在
的全体:在定义域内存在![]() ,使得
,使得![]() 成立.
成立.
(1)函数![]() 是否属于集合M?说明理由;
是否属于集合M?说明理由;
(2)设函数![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)已知函数![]() 图象与函数
图象与函数![]() 的图象有交点,根据该结论证明:函数
的图象有交点,根据该结论证明:函数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() .过
.过![]() 作一个平面
作一个平面![]() 使得
使得![]() 平面
平面![]() .
.
(1)求平面![]() 将四棱锥
将四棱锥![]() 分成两部分几何体的体积之比;
分成两部分几何体的体积之比;
(2)若平面![]() 与平面
与平面![]() 之间的距离为
之间的距离为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com