
分析 构造函数g(x)=x2f(x),求出g(x)的导数,得到函数的单调性,求出g(1+2x)>g(x),得到关于x的不等式,解出即可.
解答 解:令g(x)=x2f(x),
则g′(x)=x[xf′(x)+2f(x)],
当x>0时,xf′(x)+2f(x)>1,
故x>0时,g′(x)>0,g(x)递增,
而f(-x)=f(x),
∴g(-x)=x2f(-x)=x2f(x)=g(x),
∴g(x)是偶函数,
∴x<0时,g(x)递减,
∵f(1+2x)>($\frac{x}{1+2x}$)2•f(x),
∴(1+2x)2f(1+2x)>x2f(x),
∴g(1+2x)>g(x),
∴|1+2x|>|x|,
解得:x>-$\frac{1}{3}$或x<-1,
故不等式的解集是(-∞,-1)∪(-$\frac{1}{3}$,+∞),
故答案为:(-∞,-1)∪(-$\frac{1}{3}$,+∞).
点评 本题考查了函数的单调性、奇偶性问题,考查导数的应用,构造函数g(x)是解题的关键,本题是一道中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
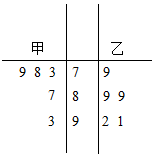 甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是$\overline{x_1},\overline{x_2}$,则下列叙述正确的是( )
甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是$\overline{x_1},\overline{x_2}$,则下列叙述正确的是( )| A. | $\overline{x_1}$>$\overline{x_2}$,乙比甲成绩稳定 | B. | $\overline{x_1}$>$\overline{x_2}$,甲比乙成绩稳定 | ||
| C. | $\overline{x_1}$<$\overline{x_2}$,乙比甲成绩稳定 | D. | $\overline{x_1}$<$\overline{x_2}$,甲比乙成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
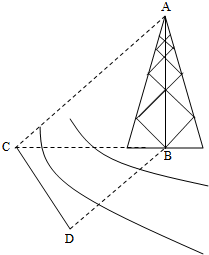 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=75°,∠BDC=45°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=75°,∠BDC=45°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )| A. | 30$\sqrt{2}$米 | B. | 30$\sqrt{6}$米 | C. | 15($\sqrt{3}$+1)米 | D. | 10$\sqrt{6}$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z | B. | x=kπ+$\frac{π}{8}$,k∈Z | C. | x=$\frac{kπ}{2}$+$\frac{3π}{8}$,k∈Z | D. | x=kπ+$\frac{3π}{8}$,k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com