
【题目】(1)求证:![]() ,其中
,其中![]() ;
;
(2)求证:![]() .
.
【答案】(1)证明见解析;
(2)证明见解析.
【解析】
(1)分别当![]() 为正偶数、正奇数时,结合二项式展开式,进行证明;
为正偶数、正奇数时,结合二项式展开式,进行证明;
(2)要证明的式子的一般形式为:![]() =
=![]() ,只要这个式子成立,那么所证明的式子也就成立.利用组合数的性质,可以证明出:右边=
,只要这个式子成立,那么所证明的式子也就成立.利用组合数的性质,可以证明出:右边=![]()
![]()
![]() ,再通过组合数的公式可以得出:
,再通过组合数的公式可以得出:![]() ,右边的式子展开,结合(1)的结论可以证明出
,右边的式子展开,结合(1)的结论可以证明出![]() ,构造数列:设
,构造数列:设![]() ,
,![]() ,利用累和法求得
,利用累和法求得![]() ,所要证明的式子成立,当
,所要证明的式子成立,当![]() ,命题得证.
,命题得证.
证明(1)当![]() 为正偶数时,
为正偶数时,
左边![]() ,
,
![]() ,
,
![]() ,
,
![]() ,所以左边=1=右边;
,所以左边=1=右边;
当![]() 为正奇数时,
为正奇数时,
左边![]() ,
,
![]() ,
,
![]() ,
,
![]() ,所以左边=1=右边.
,所以左边=1=右边.
(2)要证明的等式的一般形式为:
![]() =
=![]() ,现证明此等式成立.
,现证明此等式成立.
右边=![]()
![]()
![]()
 ,
,
![]()
![]() ,
,
由(1)可知![]() ,所以
,所以
![]() ,
,
设![]() ,
,![]() ,
,
当![]() 时,
时,![]()
![]() 时,也成立,
时,也成立,
命题得证,当![]() ,显然也成立.
,显然也成立.


科目:高中数学 来源: 题型:
【题目】如图,正方体![]() ,则下列四个命题:
,则下列四个命题:
①点![]() 在直线
在直线![]() 上运动,三棱锥
上运动,三棱锥![]() 的体积不变
的体积不变
②点![]() 在直线
在直线![]() 上运动,直线
上运动,直线![]() 与平面
与平面![]() 所成角的大小不变
所成角的大小不变
③点![]() 在直线
在直线![]() 上运动,二面角
上运动,二面角![]() 的大小不变
的大小不变
④点![]() 是平面
是平面![]() 上到点
上到点![]() 和
和![]() 距离相等的动点,则
距离相等的动点,则![]() 的轨迹是过点
的轨迹是过点![]() 的直线.
的直线.
其中的真命题是( )
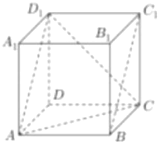
A.①③B.①③④C.①②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间x与乘客等候人数y之间的关系,经过调查得到如下数据:
间隔时间x/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
(1)从这6组数据中随机选取4组数据,求剩下的2组数据的间隔时间相邻的概率;
(2)若选取的是中间4组数据,求y关于x的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”.
,并判断此方程是否是“恰当回归方程”.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: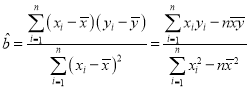 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,设直线
,设直线![]() 过椭圆
过椭圆![]() 的上顶点和右顶点,坐标原点
的上顶点和右顶点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴的正半轴上是否存在定点
轴的正半轴上是否存在定点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率之积为非零的常数?若存在,求出定点
的斜率之积为非零的常数?若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36.
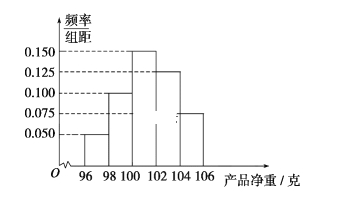
(1)求样本容量及样本中净重大于或等于96克并且小于102克的产品的个数;
(2)已知这批产品中每个产品的利润y(单位:元)与产品净重x(单位:克)的关系式为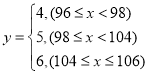 求这批产品平均每个的利润.
求这批产品平均每个的利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C是抛物线W:y2=4x上的三个点,D是x轴上一点.
(1)当点B是W的顶点,且四边形ABCD为正方形时,求此正方形的面积;
(2)当点B不是W的顶点时,判断四边形ABCD是否可能为正方形,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校工会开展健步走活动,要求教职工上传3月1日至3月7日微信记步数信息,下图是职工甲和职工乙微信记步数情况:
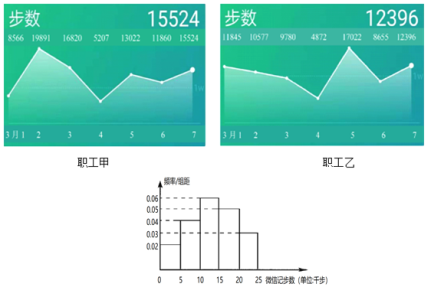
(Ⅰ)从3月1日至3月7日中任选一天,求这一天职工甲和职工乙微信记步数都不低于10000的概率;
(Ⅱ)从3月1日至3月7日中任选两天,记职工乙在这两天中微信记步数不低于10000的天数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)如图是校工会根据3月1日至3月7日某一天的数据,制作的全校200名教职工微信记步数的频率分布直方图.已知这一天甲和乙微信记步数在单位200名教职工中排名分别为第68和第142,请指出这是根据哪一天的数据制作的频率分布直方图(不用说明理由).
查看答案和解析>>
科目:高中数学 来源: 题型:
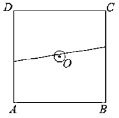
【题目】如图,正方形ABCD的边长为20米,圆O的半径为1米,圆心足正方形的中心,点P、Q分别在线段AD、CB上,若线段PQ与圆O有公共点,则称点Q在点P的“盲区”中. 已知点P以1.5米/秒的速度从A出发向D移动,同时,点Q以1米/秒的速度从C出发向B移动,则点P从A移动到D的过程中,点Q在点P的育区中的时长约为________秒(精确到0.1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以P为顶点的圆锥中,母线长为![]() ,底面圆的直径AB长为2,O为圆心.C是圆O所在平面上一点,且AC与圆O相切.连接BC交圆于点D,连接PD,PC,E是PC的中点,连接OE,ED.
,底面圆的直径AB长为2,O为圆心.C是圆O所在平面上一点,且AC与圆O相切.连接BC交圆于点D,连接PD,PC,E是PC的中点,连接OE,ED.
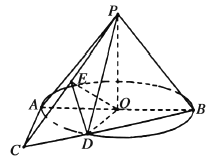
(1)求证:平面![]() 平面PAC;
平面PAC;
(2)若二面角![]() 的大小为
的大小为![]() ,求面PAC与面DOE所成锐二面角的余弦值.
,求面PAC与面DOE所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com