
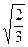 ,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段
,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段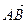 的比为2.
的比为2.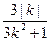 (k≠0).;(2)x2+3y2=5.
(k≠0).;(2)x2+3y2=5. 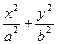 =1(a>b>0),由e=
=1(a>b>0),由e=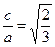 .
.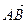 的比为2,
的比为2,
|
 ,即
,即 由
由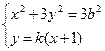 消去y整理并化简,得(3k2+1)x2+6k2x+3k2-3b2=0. 4分
消去y整理并化简,得(3k2+1)x2+6k2x+3k2-3b2=0. 4分
|
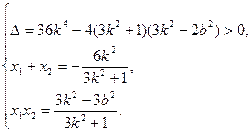 而S△OAB=
而S△OAB=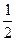 |y1-y2|=
|y1-y2|=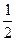 |-2y2-y2|
|-2y2-y2|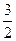 |y2|=
|y2|=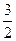 |k(x2+1)|=
|k(x2+1)|= 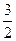 |k||x2+1|. ⑥
|k||x2+1|. ⑥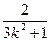 ,代入⑥得:
,代入⑥得: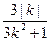 (k≠0). 8分
(k≠0). 8分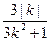 =
=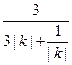 ≤
≤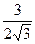 =
= ,
,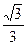 ,S△OAB取得最大值.
,S△OAB取得最大值.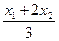 =-1,
=-1, 代入⑤得3b2=5.
代入⑤得3b2=5.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源:不详 题型:解答题

 时,求直线l的方程;
时,求直线l的方程; 为定值.
为定值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
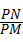 的最小值.
的最小值.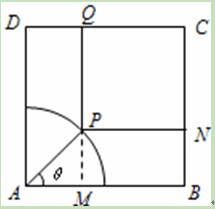
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
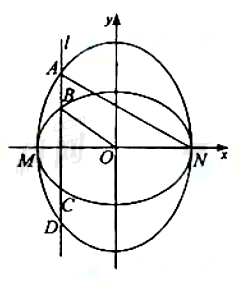
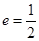 ,求
,求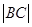 与
与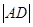 的比值;
的比值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
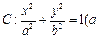 >
>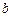 >0
>0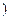 ,称圆心在原点
,称圆心在原点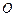 ,半径为
,半径为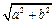 的圆是椭圆
的圆是椭圆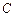 的“伴随圆”.若椭圆
的“伴随圆”.若椭圆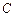 的一个焦点为
的一个焦点为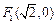 ,其短轴上的一个端点到
,其短轴上的一个端点到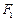 的距离为
的距离为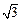 .
.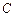 的方程及其“伴随圆”方程;
的方程及其“伴随圆”方程;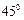 的直线
的直线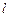 与椭圆C只有一个公共点,且与椭圆
与椭圆C只有一个公共点,且与椭圆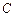 的伴随圆相交于M、N两
的伴随圆相交于M、N两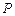 是椭圆
是椭圆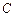 的伴随圆上的一个动点,过点
的伴随圆上的一个动点,过点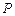 作直线
作直线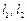 ,使得
,使得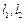 与椭圆
与椭圆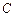 都只有一个公共点,求证:
都只有一个公共点,求证: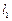 ⊥
⊥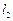 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
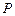 是椭圆
是椭圆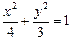 上一动点,点
上一动点,点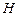 是点
是点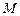 在
在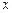 轴上的射影,坐标平面
轴上的射影,坐标平面 内动点
内动点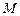 满足:
满足: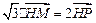 (
(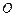 为坐标原点),设动点
为坐标原点),设动点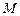 的轨迹为曲线
的轨迹为曲线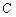 .
.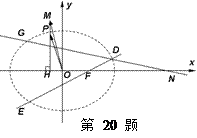
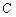 的方程并画出草图;
的方程并画出草图;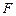 的直线
的直线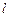 交曲线
交曲线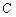 于
于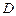 ,
,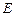 两点,且
两点,且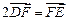 ,点
,点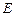 关于
关于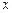 轴的对称点为
轴的对称点为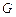 ,求直线
,求直线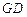 的方程.
的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com