
����Ŀ������������̳2015���Ա�����3��27���ں��ϲ����ٰ죬�����֯�߶���ļ��100������־Ը����ѵ����֯һ�� ![]() ֪ʶ�����������óɼ��Ƴ�����Ƶ�ʷֲ�ֱ��ͼ���ٶ�ÿ���������ڵijɼ����ȷֲ�������֯�ƻ��Գɼ�ǰ20���IJ����߽��н�����
֪ʶ�����������óɼ��Ƴ�����Ƶ�ʷֲ�ֱ��ͼ���ٶ�ÿ���������ڵijɼ����ȷֲ�������֯�ƻ��Գɼ�ǰ20���IJ����߽��н�����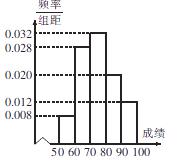
��1����ȷ���ܽ����ķ����ߣ�
��2�����ܽ�����20�������÷ֲ������ȡ5�ˣ��ٴӳ�ȡ��5���г�ȡ2�������᳡��������2�˳ɼ�����90�����ϵĸ��ʣ�
���𰸡�
��1���⣺��Ƶ�ʷֲ�ֱ��ͼ֪�������ɼ��� ![]() �ֵ�����Ϊ
�ֵ�����Ϊ ![]() �������ɼ���
�������ɼ��� ![]() ������Ϊ
������Ϊ ![]() �����ܽ�����������
�����ܽ����������� ![]() ֮�䣬���ܽ���������Ϊ
֮�䣬���ܽ���������Ϊ ![]() ����
���� ![]() �����
����� ![]() �����ܽ���������Ϊ86��
�����ܽ���������Ϊ86��
��2���⣺�ɣ�1��֪���ܽ�����20���У������� ![]() ������Ϊ8��������
������Ϊ8�������� ![]() ������Ϊ12�����÷ֲ��������֪������
������Ϊ12�����÷ֲ��������֪������ ![]() �ij�ȡ2�ˣ�������
�ij�ȡ2�ˣ������� ![]() �ij�ȡ3�ˣ��������
�ij�ȡ3�ˣ�������� ![]() ��2�˷ֱ�Ϊ
��2�˷ֱ�Ϊ ![]() ��������
�������� ![]() ��3�˷ֱ�Ϊ
��3�˷ֱ�Ϊ ![]() �����еĿ��������
�����еĿ�������� ![]() ���������������
��������������� ![]() ������ĸ���Ϊ
������ĸ���Ϊ ![]()
��������(1)���ݸ���ֱ��ͼ�����С�����������Ӧ�ĸ��ʣ�������⼴������ܽ���������Ϊ86��(2)���÷ֲ��������оٷ��ֱ����������������������еĿ�����������ø��ʵĶ��������ֵ���������ɡ�
�����㾫����������Ŀ����֪���������÷ֲ������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ�����Ƚ������е����е�λ����ij���������־���Ա�����ȣ����ֳ��������ͻ��Σ�Ȼ�����ڸ������ͻ����в��ü����������ϵ�ó����İ취��ȡһ���������������Щ���������������������������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ����С������Ϊ
����С������Ϊ ![]() ��������
�������� ![]() ��ͼ������ƽ��
��ͼ������ƽ�� ![]() ����λ���ȣ�������ƽ��
����λ���ȣ�������ƽ�� ![]() ����λ���ȣ��õ�����
����λ���ȣ��õ����� ![]() ��ͼ��.
��ͼ��.
�������� ![]() �ĵ����������䣻
�ĵ����������䣻
��������� ![]() ����
�У��� ![]() �ĶԱ߷ֱ�Ϊ
�ĶԱ߷ֱ�Ϊ ![]() .��
.�� ![]() ��
�� ![]() ����
���� ![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ͼ��Ϊ���������3n��2n��1000����Сż��n����ô�� ![]() ��
�� ![]() �����հ��У����Էֱ����루������
�����հ��У����Էֱ����루������
A.A��1000��n=n+1
B.A��1000��n=n+2
C.A��1000��n=n+1
D.A��1000��n=n+2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f(x)�Ƕ�����ΪR�����ں�������С������Ϊ2����f(1��x)��f(1��x)������1��x��0ʱ��f(x)����x.
��1���ж�f(x)����ż�ԣ�
��2�����������f(x)������[��1��2]�ϵı���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ ![]() �У�Բ
�У�Բ ![]() ��Բ
��Բ ![]() ��
��
�������� ![]() Ϊ���㣬
Ϊ���㣬 ![]() ��������Ϊ����ļ�����ϵ�У��ֱ�д��Բ
��������Ϊ����ļ�����ϵ�У��ֱ�д��Բ ![]() �ļ����귽�̣������Բ
�ļ����귽�̣������Բ ![]() �Ľ������꣨�ü������ʾ����
�Ľ������꣨�ü������ʾ����
������� ![]() ��
�� ![]() �Ĺ����ҵIJ������̣�
�Ĺ����ҵIJ������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������:����֪ ![]() ,��
,�� ![]() ��
�� ![]() ���ǡ�
���ǡ� ![]() ���ij������;
���ij������;
����֪ƽ������ ![]() ,
, ![]() �ǡ�
�ǡ� ![]() ���ı�Ҫ���������;
���ı�Ҫ���������;
����֪ ![]() ,��
,�� ![]() ���ǡ�
���ǡ� ![]() ���ij�ֲ���Ҫ����;
���ij�ֲ���Ҫ����;
������ ![]() ��
�� ![]() ,ʹ
,ʹ ![]() ��
�� ![]() ���ķ�Ϊ
���ķ�Ϊ ![]() ��
�� ![]() ,����
,���� ![]() ��
�� ![]() ��.������ȷ����ĸ����ǣ� ��
��.������ȷ����ĸ����ǣ� ��
A.0
B.1
C.2
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ǿ�߿������ѧϰ�Ĺ����ȣ������ܳɼ���ͳһ�߿������ġ���ѧ������3����Ŀ�ɼ�����ѧҵˮƽ����3����Ŀ�ɼ����.����ͳһ�߿������ġ���ѧ�������Ŀ���䣬��ֵ���䣬���������ƣ������Ŀ�ṩ���ο��Ի���.�����ܳɼ��ĸ���ѧҵˮƽ���Կ�Ŀ���ɿ������ݱ�����УҪ��������س�����˼�����Ρ���ʷ����������������ѧ�������Ϣ�����߿�Ŀ������ѡ������.
��1��ij��УijרҵҪ��ѡ����Ŀ������������Ҫ������У��רҵ�����ж�����ѡ����Ŀ��ѡ��
��2���ס��ҡ�������ͬѧ��ѡ������������ѧ����ʷ��ϣ���ѧ�Ƴɼ��ﵽ�����ĸ��ʶ���0.8��������Լ������ﵽ�������μӵڶ��ο��ԣ��ﲻ�������μӵڶ��ο��ԣ������ס��ҡ����μӵڶ��ο��Ե��ܴ���Ϊ![]() ����
����![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2018����������һ�и�����ѧ�����п�������֪��Բ![]() ��
�� ![]() ���ҽ���Ϊ
���ҽ���Ϊ![]() ����
����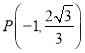 ����Բ�ϣ���
����Բ�ϣ���![]() ��
��![]() �ύ��ǡΪ
�ύ��ǡΪ![]() �е���
���
��I������Բ![]() �ķ��̣�
�ķ��̣�
��II����![]() ���������ഹֱ��ֱ�ߣ��ֱ���Բ
���������ഹֱ��ֱ�ߣ��ֱ���Բ![]() �ڵ�
�ڵ�![]() ��
��![]() �����ı���
�����ı���![]() ���������Сֵ��
���������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���Բ
�У���Բ![]() ��
�� ![]() ����������
����������![]() ����ֱ��
����ֱ��![]() ��
�� ![]() ����Բ
����Բ![]() �صõ��ҳ�Ϊ
�صõ��ҳ�Ϊ![]() ��
��
��������Բ![]() �ı����̣�
�ı����̣�
������ֱ��![]() ��Բ
��Բ![]() ��
�� ![]() ����
����
��i����Բ![]() �ı����̣�
�ı����̣�
��ii����ֱ��![]() ������
������![]() ������Բ
������Բ![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ��
��![]() ����Բ
����Բ![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ��
��![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com