
【题目】若A1,A2,…,Am为集合A={1,2,…,n}(n≥2且n∈N*)的子集,且满足两个条件:
①A1∪A2∪…∪Am=A;
②对任意的{x,y}A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}.则称集合组A1,A2,…,Am具有性质P.
如图,作n行m列数表,定义数表中的第k行第l列的数为akl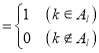 .
.
a11 | a12 | … | a1m |
a21 | a22 | … | a2m |
… | … | … | … |
an1 | an2 | … | anm |
(1)当n=4时,判断下列两个集合组是否具有性质P,如果是请画出所对应的表格,如果不是请说明理由;
集合组1:A1={1,3},A2={2,3},A3={4};
集合组2:A1={2,3,4},A2={2,3},A3={1,4}.
(2)当n=7时,若集合组A1,A2,A3具有性质P,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合A1,A2,A3;
(3)当n=100时,集合组A1,A2,…,At是具有性质P且所含集合个数最小的集合组,求t的值及|A1|+|A2|+…|At|的最小值.(其中|Ai|表示集合Ai所含元素的个数)
【答案】(1)集合组1具有性质P,集合组2不具有性质P,理由见解析;(2)图见解析,A1={3,4,5,7},A2={2,4,6,7},A3={1,5,6,7};(3)304
【解析】
(1)根据题意检验两个集合组是否满足性质即可;
(2)一共7行对应1,2,3,4,5,6,7,七个数,其中每列的1或0代表这个集合里面有或者无对应的数,要求每行必须有1,任意两个数至少有一列只出现一个;
(3)条件①可知数表M中任意一行不全为0,由条件②可得数表M中任意两行不完全相同,结合排列组合知识求解.
(1)集合组1具有性质P.
所对应的数表为:
1 | 0 | 0 |
0 | 1 | 0 |
1 | 1 | 0 |
0 | 0 | 1 |
集合组2不具有性质P.
因为存在{2,3}{1,2,3,4},有{2,3}∩A1={2,3},{2,3}∩A2={2,3},{2,3}∩A3=,
与对任意的{x,y}A,都至少存在一个i∈{1,2,3},有Ai∩{x,y}={x}或{y}矛盾,
所以集合组A1={2,3,4},A2={2,3},A3={1,4}不具有性质P.…
(2)
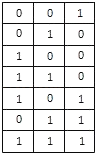
A1={3,4,5,7},A2={2,4,6,7},A3={1,5,6,7}.
(注:表格中的7行可以交换得到不同的表格,它们所对应的集合组也不同)
(3)设A1,A2,…,At所对应的数表为数表M,
因为集合组A1,A2,…,At为具有性质P的集合组,所以集合组A1,A2,…,At满足条件①和②,
由条件①:A1∪A2∪…∪At=A,可得对任意x∈A,都存在i∈{1,2,3,…,t}有x∈Ai,
所以axi=1,即第x行不全为0,所以由条件①可知数表M中任意一行不全为0.
由条件②知,对任意的{x,y}A,都至少存在一个i∈{1,2,3,…,t},使Ai∩{x,y}={x}或{y},所以axi,ayi一定是一个1一个0,即第x行与第y行的第i列的两个数一定不同.
所以由条件②可得数表M中任意两行不完全相同.
因为由0,1所构成的t元有序数组共有2t个,去掉全是0的t元有序数组,共有2t﹣1个,又因数表M中任意两行都不完全相同,所以100≤2t﹣1,所以t≥7.
又t=7时,由0,1所构成的7元有序数组共有128个,去掉全是0的数组,共127个,选择其中的100个数组构造100行7列数表,则数表对应的集合组满足条件①②,即具有性质P.所以t=7.
因为|A1|+|A2|+…+|At|等于表格中数字1的个数,
所以,要使|A1|+|A2|+…+|At|取得最小值,只需使表中1的个数尽可能少,
而t=7时,在数表M中,1的个数为1的行最多7行;1的个数为2的行最多C72=21行;1的个数为3的行最多C73=35行;1的个数为4的行最多C74=35行;
因为上述共有98行,所以还有2行各有5个1,
所以此时表格中最少有7+2×21+3×35+4×35+5×2=304个1.所以|A1|+|A2|+…+|At|的最小值为304.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
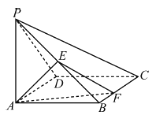
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
(1)若![]() 为线段
为线段![]() 上的动点,证明:平面
上的动点,证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() ,
,![]() ,
,![]() 上的动点(不含
上的动点(不含![]() ,
,![]() ),
),![]() ,三棱锥
,三棱锥![]() 的体积是否存在最大值?如果存在,求出最大值;如果不存在,请说明理由.
的体积是否存在最大值?如果存在,求出最大值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
日均浓度 |
|
|
|
|
|
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
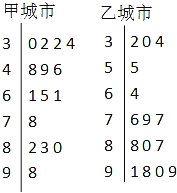
(Ⅰ)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(Ⅱ)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(Ⅲ)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 的内切圆与三边
的内切圆与三边![]() 的切点分别为
的切点分别为![]() ,已知
,已知![]() ,内切圆圆心
,内切圆圆心![]() ,设点A的轨迹为R.
,设点A的轨迹为R.
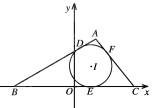
(1)求R的方程;
(2)过点C的动直线m交曲线R于不同的两点M,N,问在x轴上是否存在一定点Q(Q不与C重合),使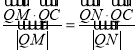 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区甲、乙、丙三所单位进行招聘,其中甲单位招聘2名,乙单位招聘2名,丙单位招聘1名,并且甲单位要至少招聘一名男生,现有3男3女参加三所单位的招聘,则不同的录取方案种数为( )
A.36B.72C.108D.144
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对其定义域内的任意
对其定义域内的任意![]() ,
,![]() ,当
,当![]() 时总有
时总有![]() ,则称
,则称![]() 为紧密函数,例如函数
为紧密函数,例如函数![]() 是紧密函数,下列命题:
是紧密函数,下列命题:
![]() 紧密函数必是单调函数;
紧密函数必是单调函数;![]() 函数
函数![]() 在
在![]() 时是紧密函数;
时是紧密函数;
![]() 函数
函数![]() 是紧密函数;
是紧密函数;
![]() 若函数
若函数![]() 为定义域内的紧密函数,
为定义域内的紧密函数,![]() ,则
,则![]() ;
;
![]() 若函数
若函数![]() 是紧密函数且在定义域内存在导数,则其导函数
是紧密函数且在定义域内存在导数,则其导函数![]() 在定义域内的值一定不为零.
在定义域内的值一定不为零.
其中的真命题是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】裴波那契数列(Fibonacci sequence )又称黄金分割数列,因为数学家列昂纳多·裴波那契以兔子繁殖为例子引入,故又称为“兔子数列”,在数学上裴波那契数列被以下递推方法定义:数列![]() 满足:
满足:![]() ,
,![]() ,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com