已知f(x)=-3x2+a(6-a)x+b.
(1)解关于a的不等式f(1)>0;
(2)当不等式f(x)>0的解集为(-1,3)时,求实数a,b的值.
解:(1)f(1)=-3+a(6-a)+b=-a
2+6a+b-3,∵f(1)>0,∴a
2-6a+3-b<0.
△=24+4b,当△≤0,即b≤-6时,f(1)>0 的解集为∅;
当b>-6时,3-
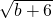
<a<3+
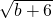
,
∴f(1)>0的解集为{a|3-
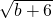
<a<3+
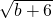
}.
(2)∵不等式-3x
2+a(6-a)x+b>0的解集为(-1,3),
∴
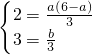
解之,得
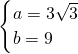
.
分析:(1)不等式即 a
2-6a+3-b<0,当△≤0 时,解集为∅;△>0时,解得 3-
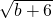
<a<3+
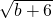
.
(2)由题意知,-1和3是方程-3x
2+a(6-a)x+b=0 的两个根,由根与系数的关系得
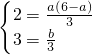
,解之可得结果.
点评:本题考查一元二次不等式的解法,一元二次方程根与系数的关系,体现了分类讨论的数学思想.

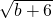 <a<3+
<a<3+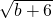 ,
,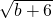 <a<3+
<a<3+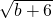 }.
}.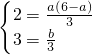 解之,得
解之,得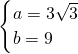 .
.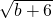 <a<3+
<a<3+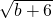 .
.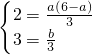 ,解之可得结果.
,解之可得结果.
