
【题目】如图,在三棱柱![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 的中点.
的中点.
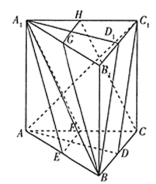
(1)求证:![]() 、
、![]() 、
、![]() 、
、![]() 四点共面;
四点共面;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() .
.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)证明出![]() ,即可证明出
,即可证明出![]() 、
、![]() 、
、![]() 、
、![]() 四点共面;
四点共面;
(2)证明![]() ,可得
,可得![]() 平面
平面![]() ,证明四边形
,证明四边形![]() 是平行四边形,可得出
是平行四边形,可得出![]() ,可证明出
,可证明出![]() 平面
平面![]() ,再利用面面平行的判定定理可证明出结论;
,再利用面面平行的判定定理可证明出结论;
(3)连接![]() 交
交![]() 于点
于点![]() ,可得出
,可得出![]() ,可证明出
,可证明出![]() 平面
平面![]() ,证明出四边形
,证明出四边形![]() 为平行四边形,可得出
为平行四边形,可得出![]() ,可得出
,可得出![]() 平面
平面![]() ,然后利用面面平行的判定定理可证明出结论.
,然后利用面面平行的判定定理可证明出结论.
(1)![]() 是
是![]() 的中位线,
的中位线,![]() .
.
在三棱柱![]() 中,
中,![]() 且
且![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,![]() ,因此,
,因此,![]() 、
、![]() 、
、![]() 、
、![]() 四点共面;
四点共面;
(2)![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
在三棱柱![]() 中,
中,![]() 且
且![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
![]() 且
且![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,则
是平行四边形,则![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
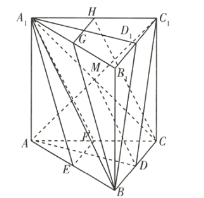
(3)如图所示,连接![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,连接
,连接![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() 是
是![]() 的中点,
的中点,
![]() 为
为![]() 的中点,
的中点,![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
由(1)知,四边形![]() 为平行四边形,则
为平行四边形,则![]() 且
且![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,所以,
的中点,所以,![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
,![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂共有男女员工500人,现从中抽取100位员工对他们每月完成合格产品的件数统计如下:
每月完成合格产品的件数(单位:百件) |
|
|
|
|
|
频数 | 10 | 45 | 35 | 6 | 4 |
男员工人数 | 7 | 23 | 18 | 1 | 1 |
(1)其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面![]() 列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
非“生产能手” | “生产能手” | 合计 | |
男员工 | |||
span>女员工 | |||
合计 |
(2)为提高员工劳动的积极性,工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的,计件单价为1元;超出![]() 件的部分,累进计件单价为1.2元;超出
件的部分,累进计件单价为1.2元;超出![]() 件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
附:![]() ,
,
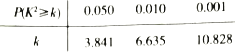 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=e2x﹣ax2+1在[1,2]上是减函数,则实数a的取值范围是( )
A. [![]() ,+∞) B. (
,+∞) B. (![]() ,+∞) C. [
,+∞) C. [![]() ,+∞) D. (
,+∞) D. (![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国民法总则》(以下简称《民法总则》)自2017年10月1日起施行.作为民法典的开篇之作,《民法总则》与每个人的一生息息相关.某地区为了调研本地区人们对该法律的了解情况,随机抽取50人,他们的年龄都在区间![]() 上,年龄的频率分布及了解《民法总则》的入数如下表:
上,年龄的频率分布及了解《民法总则》的入数如下表:
年龄 |
|
|
|
|
|
|
频数 | 5 | 5 | 10 | 15 | 5 | 10 |
了解《民法总则》 | 1 | 2 | 8 | 12 | 4 | 5 |
(1)填写下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为以45岁为分界点对了解《民法总则》政策有差异;
的把握认为以45岁为分界点对了解《民法总则》政策有差异;
年龄低于45岁的人数 | 年龄不低于45岁的人数 | 合计 | |
了解 |
|
| |
不了解 |
|
| |
合计 |
(2)若对年龄在![]() ,
,![]() 的被调研人中各随机选取2人进行深入调研,记选中的4人中不了解《民法总则》的人数为
的被调研人中各随机选取2人进行深入调研,记选中的4人中不了解《民法总则》的人数为![]() ,求随机变量的分布列和数学期望.
,求随机变量的分布列和数学期望.
参考公式和数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为![]() ,
,![]() ,
,![]() ,假设各盘比赛结果相互独立.
,假设各盘比赛结果相互独立.
(I)求红队至少两名队员获胜的概率;
(II)用![]() 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com