
 ,则
,则 •
• 的取值范围为
的取值范围为 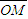 •
•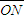 =2x+y,设z=2x+y,再利用几何意义求范围,将范围问题转化为y轴上的截距,只需求出直线z=2x+y,过可行域内的点A(3,9)时的最大值,从而得到z最大值即可.同样可求出z的最小值,从而问题解决.
=2x+y,设z=2x+y,再利用几何意义求范围,将范围问题转化为y轴上的截距,只需求出直线z=2x+y,过可行域内的点A(3,9)时的最大值,从而得到z最大值即可.同样可求出z的最小值,从而问题解决. 解:如图可行域为阴影部分,
解:如图可行域为阴影部分,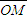 •
•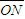 =2x+y,设z=2x+y,
=2x+y,设z=2x+y,

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:《第3章 不等式》2010年单元测试卷(5)(解析版) 题型:选择题
 ,则z=2x+y的最大值为 ( )
,则z=2x+y的最大值为 ( )查看答案和解析>>
科目:高中数学 来源:2011年辽宁省名校领航高考数学预测试卷(五)(解析版) 题型:选择题
 ,则z=2x+y的最大值为 ( )
,则z=2x+y的最大值为 ( )查看答案和解析>>
科目:高中数学 来源:2010年山东省潍坊市高考数学模拟试卷A(理科)(解析版) 题型:选择题
 ,则z=2x+y的最大值为 ( )
,则z=2x+y的最大值为 ( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com