
已知扇形的周长为30,当它的半径R和圆心角 各取何值时,扇形的面积S最大?并求出扇形面积的最大值.
各取何值时,扇形的面积S最大?并求出扇形面积的最大值.
当扇形半径为 ,圆心角为2时,扇形有最大面积
,圆心角为2时,扇形有最大面积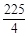 .
.
解析试题分析:根据条件扇形的周长为30可以得到l+2R=30,从而扇形的面积S=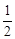 lR=
lR=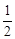 (30-2R)R=
(30-2R)R=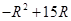 ,即把S表示为R的二次函数,根据二次函数求最值的方法,可以进一步变形为
,即把S表示为R的二次函数,根据二次函数求最值的方法,可以进一步变形为
S=-(R- )2+
)2+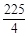 ,从而得到当扇形半径为
,从而得到当扇形半径为 ,圆心角为2时,扇形有最大面积
,圆心角为2时,扇形有最大面积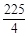 .
.
∵扇形的周长为30,∴l+2R=30,l=30-2R,
∴S=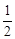 lR=
lR=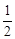 (30-2R)R=
(30-2R)R=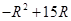 =-(R-
=-(R- )2+
)2+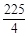 .....5分
.....5分
∴当R= 时,扇形有最大面积
时,扇形有最大面积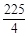 ,此时l=30-2R=15,
,此时l=30-2R=15, =
=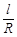 =2........8分
=2........8分
答:当扇形半径为 ,圆心角为2时,扇形有最大面积
,圆心角为2时,扇形有最大面积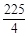 .....10分.
.....10分.
考点:1、弧度制下扇形相关公式;2、二次函数求最值.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
如图,某污水处理厂要在一正方形污水处理池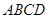 内修建一个三角形隔离区以投放净化物质,其形状为三角形
内修建一个三角形隔离区以投放净化物质,其形状为三角形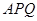 ,其中
,其中 位于边
位于边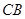 上,
上,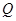 位于边
位于边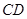 上.已知
上.已知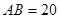 米,
米,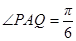 ,设
,设 ,记
,记 ,当
,当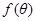 越大,则污水净化效果越好.
越大,则污水净化效果越好.
(1)求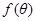 关于的函数解析式,并求定义域;
关于的函数解析式,并求定义域;
(2)求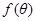 最大值,并指出等号成立条件?
最大值,并指出等号成立条件?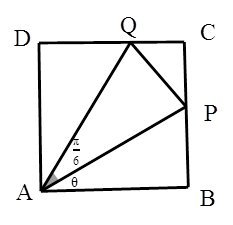
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2014·济南模拟)已知函数f(x)=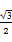 sinωx-sin2
sinωx-sin2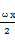 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值及函数f(x)的单调递增区间.
(2)当x∈ 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com