
【题目】已知f(x)=e2x+ln(x+a).
(1)当a=1时,①求f(x)在(0,1)处的切线方程;②当x≥0时,求证:f(x)≥(x+1)2+x.
(2)若存在x0∈[0,+∞),使得 ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
【答案】
(1)解:a=1时,f(x)=e2x+ln(x+1),f′(x)=2e2x+ ![]() ,
,
①可得f(0)=1,f′(0)=2+1=3,
所以f(x)在(0,1)处的切线方程为y=3x+1;
②证明:设F(x)=e2x+ln(x+1)﹣(x+1)2﹣x(x≥0),
F′(x)=2e2x+ ![]() ﹣2(x+1)﹣1
﹣2(x+1)﹣1
F″(x)=4e2x﹣ ![]() ﹣2=[e2x﹣﹣
﹣2=[e2x﹣﹣ ![]() ]+2(e2x﹣1)+e2x>0,(x≥0),
]+2(e2x﹣1)+e2x>0,(x≥0),
所以,F′(x)在[0,+∞)上递增,所以F′(x)≥F′(0)=0,
所以,F(x)在[0,+∞)上递增,所以F(x)≥F(0)=0,
即有当x≥0时,f(x)≥(x+1)2+x
(2)解:存在x0∈[0,+∞),使得 ![]() 成立
成立
存在x0∈[0,+∞),使得e ![]() ﹣ln(x0+a)﹣x02<0,
﹣ln(x0+a)﹣x02<0,
设u(x)=e2x﹣ln(x+a)﹣x2,
u′(x)=2e2x﹣ ![]() ﹣2x,u″(x)=4e2x+
﹣2x,u″(x)=4e2x+ ![]() ﹣2>0,
﹣2>0,
可得u′(x)在[0,+∞)单调增,即有u′(x)≥u′(0)=2﹣ ![]()
①当a≥ ![]() 时,u′(0)=2﹣
时,u′(0)=2﹣ ![]() ≥0,
≥0,
可得u(x)在[0,+∞)单调增,
则u(x)min=u(0)=1﹣lna<0,
解得a>e;
②当a< ![]() 时,ln(x+a)<ln(x+
时,ln(x+a)<ln(x+ ![]() ),
),
设h(x)=x﹣ ![]() ﹣ln(x+
﹣ln(x+ ![]() ),(x>0),
),(x>0),
h′(x)=1﹣ ![]() =
= ![]() ,
,
另h′(x)>0可得x> ![]() ,h′(x)<0可得0<x<
,h′(x)<0可得0<x< ![]() ,
,
则h(x)在(0, ![]() )单调递减,在(
)单调递减,在( ![]() ,+∞)单调递增.
,+∞)单调递增.
则h(x)≥h( ![]() )=0./p>
)=0./p>
设g(x)=e2x﹣x2﹣(x﹣ ![]() ),(x>0),
),(x>0),
g′(x)=2e2x﹣2x﹣1,
g″(x)=4e2x﹣2>4﹣2>0,
可得g′(x)在(0,+∞)单调递增,
即有g′(x)>g′(0)=1>0,
则g(x)在(0,+∞)单调递增,
则g(x)>g(0)>0,
则e2x﹣x2>x﹣ ![]() >ln(x+
>ln(x+ ![]() )>ln(x+a),
)>ln(x+a),
则当a< ![]() 时,f(x)>2ln(x+a)+x2恒成立,不合题意.
时,f(x)>2ln(x+a)+x2恒成立,不合题意.
综上可得,a的取值范围为(e,+∞)
【解析】(1)①求出f(x)的导数,可得切线的斜率,由斜截式方程即可得到所求切线的方程;②设F(x)=e2x+ln(x+1)﹣(x+1)2﹣x(x≥0),通过两次求导,判断F(x)的单调性,即可得证;(2)由题意可得存在x0∈[0,+∞),使得e ![]() ﹣ln(x0+a)﹣x02<0,设u(x)=e2x﹣ln(x+a)﹣x2 , 两次求导,判断单调性,对a讨论,分①当a≥
﹣ln(x0+a)﹣x02<0,设u(x)=e2x﹣ln(x+a)﹣x2 , 两次求导,判断单调性,对a讨论,分①当a≥ ![]() 时,②当a<
时,②当a< ![]() 时,通过构造函数和求导,得到单调区间,可得最值,即可得到所求a的范围.
时,通过构造函数和求导,得到单调区间,可得最值,即可得到所求a的范围.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
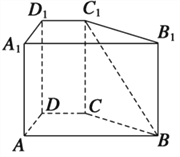
【题目】如图,已知直四棱柱ABCD—A1B1C1D1中,AA1=2,底面ABCD是直角梯形,∠A为直角,AB∥CD,AB=4,AD=2,DC=2.
(Ⅰ)求线段BC1的长度;
(Ⅱ)异面直线BC1与DC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() cos(2x-
cos(2x-![]() ),x∈R.
),x∈R.
(1)求函数f(x)的最小正周期和单调递减区间;
(2)求函数f(x)在区间[-![]() ,
,![]() ]上的最小值和最大值,并求出取得最值时x的值.
]上的最小值和最大值,并求出取得最值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查甲、乙两种品牌商品的市场认可度,在某购物网点随机选取了14天,统计在某确定时间段的销量,得如下所示的统计图,根据统计图求:
(1)甲、乙两种品牌商品销量的中位数分别是多少?
(2)甲品牌商品销量在[20,50]间的频率是多少?
(3)甲、乙两个品牌商品哪个更受欢迎?并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中心在原点的椭圆C1与双曲线C2具有相同的焦点,F1(﹣c,0),F2(c,0),P为C1与C2在第一象限的交点,|PF1|=|F1F2|且|PF2|=5,若椭圆C1的离心率 ![]() ,则双曲线的离心率e2的范围是( )
,则双曲线的离心率e2的范围是( )
A.![]()
B.![]()
C.(2,3)
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() 的顶点,
的顶点, ![]() 为椭圆
为椭圆![]() 的左焦点且椭圆
的左焦点且椭圆![]() 经过点
经过点 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右顶点
的右顶点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,连结
,连结![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,当
,当![]() 的面积取得最大值时,求
的面积取得最大值时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 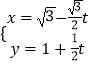 (t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,圆C的极坐标方程为
(t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,圆C的极坐标方程为 ![]() .
.
(1)求圆C的直角坐标方程;
(2)若P(x,y)是直线l与圆面 ![]() 的公共点,求
的公共点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com