
【题目】甲参加A , B , C三个科目的学业水平考试,其考试成绩合格的概率如下表,假设三个科目的考试甲是否成绩合格相互独立.
科目A | 科目B | 科目C | |
甲 |
|
|
|
(I)求甲至少有一个科目考试成绩合格的概率;
(Ⅱ)设甲参加考试成绩合格的科目数量为X , 求X的分布列和数学期望.
【答案】解:(I)记“甲至少有一个科目考试成绩合格”为事件M,
则P( ![]() )=(1-
)=(1- ![]() )×(1-
)×(1- ![]() )×(1-
)×(1- ![]() )=
)= ![]() ,
,
所以P(M)=1-P( ![]() )=
)= ![]() ,
,
(II)依题意X=0,1,2,3.
P(X=0)=(1- ![]() )×(1-
)×(1- ![]() )×(1-
)×(1- ![]() )=
)= ![]() ;
;
P(X=1)= ![]() ×(1-
×(1- ![]() )×(1-
)×(1- ![]() )+(1-
)+(1- ![]() )×
)× ![]() ×(1-
×(1- ![]() )+(1-
)+(1- ![]() )×(1-
)×(1- ![]() )×
)× ![]() =
= ![]() =
= ![]() ;
;
P(X=3)= ![]() ×
× ![]() ×
× ![]() =
= ![]() =
= ![]() ;
;
P(X=2)=1-P(X=0)-P(X=1)-P(X=3)= ![]() .
.
所以,随机变量X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
EX=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =
= ![]()
【解析】(1)根据题意利用对立事件的概率求出“甲至少有一个科目考试成绩合格”的概率。(2)由已知求出X的取值为0,1,2,3,结合概率的定义分别求出各个X值对应的概率值列表即可,再把数值代入数学期望公式求出即可。


科目:高中数学 来源: 题型:
【题目】给出下面三个类比结论:①向量 ![]() ,有
,有 ![]() ;类比复数
;类比复数 ![]() ,有
,有 ![]() ;
;
②实数 ![]() 、
、 ![]() 有
有 ![]() ;类比向量
;类比向量 ![]() ,有
,有 ![]() ;
;
③实数 ![]() 、
、 ![]() 有
有 ![]() ,则
,则 ![]() ;类比复数
;类比复数 ![]() ,有
,有 ![]() ,则
,则 ![]() .其中类比结论正确的命题个数为 ( )
.其中类比结论正确的命题个数为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”下图是根据刘徽的“割圆术”思想设计的一个程序框图.若运行该程序,则输出的n的值为:(参考数据: ![]() ≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( )
≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( ) 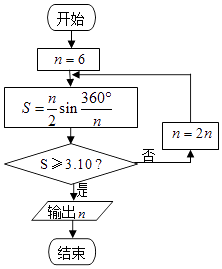
A.48
B.36
C.30
D.24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对大学生毕业后自主创业人员给予小额贷款补贴,贷款期限分为6个月、12个月、18个月、24个月、36个月五种,对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元,从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计,选取贷款期限的频数如表:
贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
频数 | 20 | 40 | 20 | 10 | 10 |
以上表中各种贷款期限的频数作为2017年自主创业人员选择各种贷款期限的概率.
(Ⅰ)某大学2017年毕业生中共有3人准备申报此项贷款,计算其中恰有两人选择贷款期限为12个月的概率;
(Ⅱ)设给某享受此项政策的自主创业人员补贴为X元,写出X的分布列;该市政府要做预算,若预计2017年全市有600人申报此项贷款,则估计2017年该市共要补贴多少万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在D上的函数 ![]() ,若满足:
,若满足: ![]() ,都有
,都有 ![]() 成立,则称
成立,则称 ![]() 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数 ![]() 的上界.
的上界.
(I)设 ![]() ,证明:
,证明: ![]() 在
在 ![]() 上是有界函数,并写出
上是有界函数,并写出 ![]() 所有上界的值的集合;
所有上界的值的集合;
(II)若函数 ![]() 在
在 ![]() 上是以3为上界的有界函数,求实数a的取值范围.
上是以3为上界的有界函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)如图所示的茎叶图记录了甲、乙两组各四名同学的投篮命中次数, 乙组记录中有一个数据模糊,无法确认, 在图中以![]() 表示.
表示.

(Ⅰ)如果乙组同学投篮命中次数的平均数为![]() , 求
, 求![]() 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(Ⅱ)在(Ⅰ)的条件下, 分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名, 记事件A:“两名同学的投篮命中次数之和为17”, 求事件A发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com