
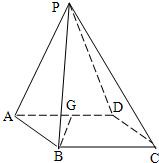
 20、P是四边形ABCD所在平面外一点,ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
20、P是四边形ABCD所在平面外一点,ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD.

 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
 图1所示是某高速公路收费站入口处的安全标识墩.墩的下半部分是长方体ABCD-EFGH,上半部分是四棱锥P-ABCD,点P在面ABCD上的投影是四边形ABCD的中心,图2、图3分别是该标识墩的正(主)视图和俯视图(尺寸如图,单位:cm).
图1所示是某高速公路收费站入口处的安全标识墩.墩的下半部分是长方体ABCD-EFGH,上半部分是四棱锥P-ABCD,点P在面ABCD上的投影是四边形ABCD的中心,图2、图3分别是该标识墩的正(主)视图和俯视图(尺寸如图,单位:cm).查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:江西省白鹭洲中学2008-2009学年高二下学期第一次月考(数学) 题型:022
如图所示,P是四边形ABCD所在平面外一点,O是AC与BD的交点,且PO⊥平面ABCD.当四边形ABCD满足下列条件________时,点P到四边形四条边的距离相等.①正方形;②圆的外切四边形;③菱形;④矩形.

查看答案和解析>>
科目:高中数学 来源:云南省芒市中学2011-2012学年高二上学期期末考试数学试题 题型:044
如图,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,

(1)求证:BG⊥平面PAD;
(2)求PB与面ABCD所成角.
查看答案和解析>>
科目:高中数学 来源:2013届云南省芒市高二上学期期末考试数学试卷 题型:解答题
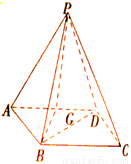
如图,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为 的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,
的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,
⑴求证:BG⊥平面PAD;
⑵求PB与面ABCD所成角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com