
【题目】设函数f(x)=|x+2|﹣|x﹣1|
(I)画出函数y=f(x)的图象;
(II)若关于x的不等式f(x)+4≥|1﹣2m|有解,求实数m的取值范围.
【答案】解:(I)函数f(x)可化为:…3′
其图象如下:…5′
(II)关于x的不等式f(x)+4≥|1﹣2m|有解等价于:
(f(x)+4)max≥|1﹣2m|.…6′
由(I)可知f(x)max=3,
(也可由|f(x)|=||x+2|﹣|x﹣1||≤|(x+2)﹣(x﹣1|)|=3,得f(x)max=3)…8′
于是|1﹣2m|≤7,
解得实数m的取值范围:m∈[﹣3,4]…10′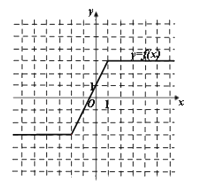
【解析】(I)先将原函数式可化为一个分段函数的形式,再分段画出函数在各段上的图象即得原函数的图象.
(II)关于x的不等式f(x)+4≥|1﹣2m|有解等价于:(f(x)+4)max≥|1﹣2m|,再根据分段函数的图象,确定函数的最大值,从而可求实数m的取值范围.
【考点精析】认真审题,首先需要了解函数的值(函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法).


科目:高中数学 来源: 题型:
【题目】某商场预计全年分批购入每台价值为2000元的电视机共3600台.每批都购入![]() 台
台![]() ,且每批均需付运费400元.贮存购入所有的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比,比例系数为
,且每批均需付运费400元.贮存购入所有的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比,比例系数为![]() ,若每批购入400台,则全年需用去运输和保管总费用43600元.
,若每批购入400台,则全年需用去运输和保管总费用43600元.
(1)求![]() 的值;
的值;
(2)现在全年只有24000元资金用于支付这笔费用,请问能否恰当安排每批进货的数量使资金够用?写出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
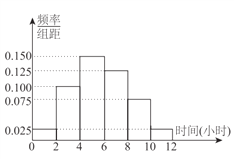
【题目】某中学共有5000人,其中男生3500人,女生1500人,为了了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关,现在用分层抽样的方法从中收集300位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如下:
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
已知在样本数据中,有60位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理,我们( )
A. 没有理由认为“该校学生每周平均体育锻炼时间与性别有关”
B. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别无关”
的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex·(a+![]() +lnx),其中a∈R.
+lnx),其中a∈R.
(I)若曲线y=f(x)在x=1处的切线与直线y=-![]() 垂直,求a的值;
垂直,求a的值;
(II)当a∈(0,ln2)时,证明:f(x)存在极小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
,![]() ,
,![]() ,
,![]() 是实数常数,
是实数常数,![]() ).
).
(1)若![]() ,函数
,函数![]() 的图象关于点
的图象关于点![]() 成中心对称,求
成中心对称,求![]() ,
,![]() 的值;
的值;
(2)若函数![]() 满足条件(1),且对任意
满足条件(1),且对任意![]() ,总有
,总有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() ,函数
,函数![]() 是奇函数,
是奇函数,![]() ,
,![]() ,且对任意
,且对任意![]() 时,不等式
时,不等式![]() 恒成立,求负实数
恒成立,求负实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数y=sin(2x+![]() )的图象向右平移
)的图象向右平移![]() 个单位,再把所得图象上各点的横坐标缩短到原来的
个单位,再把所得图象上各点的横坐标缩短到原来的![]() , 则所得图象的函数解析式是( )
, 则所得图象的函数解析式是( )
A.y=sin(4x+![]() π)
π)
B.y=sin(4x+![]() )
)
C.y=sin4x
D.y=sinx
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高一新生分成水平相同的甲、乙两个平行班,每班50人,某教师采用![]() 、
、![]() 两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.
两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.

(1)在乙班的20个个体中,从不低于86分的成绩中随机抽取2人,求抽出的两个人均“成绩优秀”的概率;
(2)由以上统计数据填写![]() 列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
甲班( | 乙班( | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.847 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com