求直线y=2x+3与抛物线y=x2所围成的图形的面积S= .
【答案】
分析:本题考查的知识点是定积分的几何意义,首先我们要联立两个曲线的方程,判断他们的交点,以确定积分公式中x的取值范围,再根据定积分的几何意义,所求图形的面积为S=∫
-13(2x+3)dx-∫
-13x
2dx,计算后即得答案.
解答:解:由方程组

解得,x
1=-1,x
2=3.
故所求图形的面积为S=∫
-13(2x+3)dx-∫
-13x
2dx
=20-
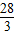
=

故答案为:
 点评:
点评:在直角坐标系下平面图形的面积的四个步骤:1.作图象;2.求交点;3.用定积分表示所求的面积;4.微积分基本定理求定积分.

 阅读快车系列答案
阅读快车系列答案