
【题目】已知![]() .
.
(1)求![]() 的图象是由
的图象是由![]() 的图象如何变换而来?
的图象如何变换而来?
(2)求![]() 的最小正周期、图象的对称轴方程、最大值及其对应的
的最小正周期、图象的对称轴方程、最大值及其对应的![]() 的集合.
的集合.
【答案】(1)见解析;(2)![]() ;
;![]() ,
,![]() ;2;
;2;![]()
【解析】
(1)由条件根据函数![]() 的图象平移伸缩的变换规律,可得结论.
的图象平移伸缩的变换规律,可得结论.
(2)根据题意,利用正弦函数的最小正周期![]() ,结合正弦函数的图象和性质,即可求出
,结合正弦函数的图象和性质,即可求出![]() 的对称轴、最大值.
的对称轴、最大值.
解:(1)将函数![]() 图象上每一点的横坐标不变,纵坐标伸长到原来的3倍,
图象上每一点的横坐标不变,纵坐标伸长到原来的3倍,
得到函数![]() 的图象,
的图象,
再把所得函数图象上每一点的横坐标缩短为原来的![]() 倍(纵坐标不变),
倍(纵坐标不变),
得到函数![]() 的图象,
的图象,
再把所得函数的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,
的图象,
最后把所得函数的图象向下平移1个单位长度,得到函数![]() 的图象.
的图象.
(2)对于函数![]() ,它的最小正周期为
,它的最小正周期为![]() ,
,
由![]() ,
,![]() ,求得
,求得![]() ,
,
可得函数的图象的对称轴方程为:![]() ,
,![]() ,
,
由![]() ,
,![]() ,求得
,求得![]() ,
,![]() ,
,
此时![]() 的最大值为
的最大值为![]() ,即对应的
,即对应的![]() 的集合为
的集合为![]() .
.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为边长为2的菱形,
为边长为2的菱形,![]() ,
,![]() ,面
,面![]() 面
面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
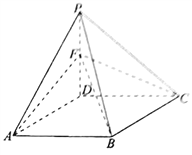
(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 面
面![]() ,并说明理由;
,并说明理由;
(2)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ’(
’(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·湖北襄阳模拟)已知椭圆C:![]() (a>b>0)的焦点为F1,F2,P是椭圆C上一点,若PF1⊥PF2,|F1F2|=2
(a>b>0)的焦点为F1,F2,P是椭圆C上一点,若PF1⊥PF2,|F1F2|=2![]() ,△PF1F2的面积为1.
,△PF1F2的面积为1.
(1)求椭圆C的方程;
(2)如果椭圆C上总存在关于直线y=x+m对称的两点A,B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正四棱锥![]() 中,
中,![]() 为底面正方形的中心,侧棱
为底面正方形的中心,侧棱![]() 与底面
与底面![]() 所成的角的正切值为
所成的角的正切值为![]() .
.

(1)求侧面![]() 与底面
与底面![]() 所成的二面角的大小;
所成的二面角的大小;
(2)若![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的正切值;
所成角的正切值;
(3)问在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ⊥侧面
⊥侧面![]() ,若存在,试确定点
,若存在,试确定点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下:
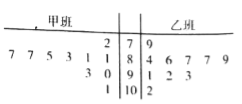
(Ⅰ)根据茎叶图,计算甲班被抽取学生成绩的平均值![]() 及方差
及方差![]() ;
;
(Ⅱ)若规定成绩不低于90分的等级为优秀,现从甲、乙两个班级所抽取成绩等级为优秀的学生中,随机抽取2人,求这两个人恰好都来自甲班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com