
分析 (1)由已知中函数的解析式,可得f(x)是R上的奇函数,且在R上单调递增.
(2)由题意可得 f(1-m)<-f(1-m2)=f(m2-1),故有-1<1-m<m2-1<1,由此解得m的范围.
(3)要使f(x)-4的值恒为负,只要f(2)-4≤0,即 $\frac{a}{{{a^2}-1}}({{a^2}-{a^{-2}}})-4=\frac{{{a^2}+1}}{a}-4≤0$,由此求得a的范围.
解答 解:(1)∵函数f(x)=$\frac{a}{{{a^2}-1}}({{a^x}-{a^{-x}}})$,
∴f(x)是R上的奇函数,且在R上单调递增.
(2)由f(x)的奇偶性可得 f(1-m)<-f(1-m2)=f(m2-1),
由f(x)的定义域及单调性可得-1<1-m<m2-1<1.
解不等式组可得 $1<m<\sqrt{2}$.
(3)由于f(x)在(-∞,2)上单调递增,要f(x)-4恒负,
只需f(2)-4≤0,
即$\frac{a}{{{a^2}-1}}({{a^2}-{a^{-2}}})-4=\frac{{{a^2}+1}}{a}-4≤0$
解之得:$2-\sqrt{3}≤a≤2+\sqrt{3}$.
结合a>0且a≠1可得:$2-\sqrt{3}≤a≤2+\sqrt{3}$且a≠1.
点评 本题主要考查函数的单调性和奇偶性,利用函数的单调性解不等式,属于中档题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:解答题
 三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=$\sqrt{13}$,SB=$\sqrt{29}$,
三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=$\sqrt{13}$,SB=$\sqrt{29}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7$\frac{1}{3}$,PO=12,则AB=16.
如图,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7$\frac{1}{3}$,PO=12,则AB=16.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{5}$ | B. | $\sqrt{15}$ | C. | 3 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
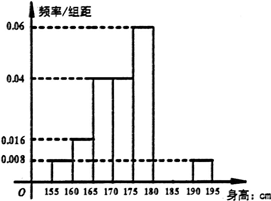 某学校进行体检,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50人身材介于155cm到195cm之间),现将抽取结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],并按此分组绘制如下图所示的频率分布直方图,其中,第六组和第七组还没有绘制完成,已知第一组与第八组人数相同,第七组的人数为3人.
某学校进行体检,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50人身材介于155cm到195cm之间),现将抽取结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],并按此分组绘制如下图所示的频率分布直方图,其中,第六组和第七组还没有绘制完成,已知第一组与第八组人数相同,第七组的人数为3人.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com