
| 1 | ||
|
| m |
| 2 |
| n |
| 2 |


科目:高中数学 来源: 题型:
| 3 |
| x+2 |
| 30 |
| s |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 使用年限x(年) | 2 | 3 | 4 | 5 | 6 |
| 维修费用y(元) | 2.2 | 3.8 | 5.5 | 6.5 | 7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
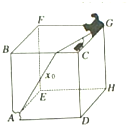 一位电脑爱好者设计了一个“猫捉老鼠”的动画游戏,如图所示,在一个边长为a的大正方体木箱的一个顶点G上,老鼠从猫的爪间逃出,沿着木箱的棱边奔向洞口,洞口子在方木箱的另一顶点A处,若老鼠在奔跑中,并不重复跳过任意一条棱边,也不再回到G点,聪明的猫也选择了一条最短的路程奔向洞口(设猫和老鼠同时从G点出发),结果猫再次在洞口A捉住了老鼠,问:
一位电脑爱好者设计了一个“猫捉老鼠”的动画游戏,如图所示,在一个边长为a的大正方体木箱的一个顶点G上,老鼠从猫的爪间逃出,沿着木箱的棱边奔向洞口,洞口子在方木箱的另一顶点A处,若老鼠在奔跑中,并不重复跳过任意一条棱边,也不再回到G点,聪明的猫也选择了一条最短的路程奔向洞口(设猫和老鼠同时从G点出发),结果猫再次在洞口A捉住了老鼠,问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com