
【题目】已知函数f(x)=(m2+2m) ![]() ,当m为何值时f(x)是:
,当m为何值时f(x)是:
(1)正比例函数?
(2)反比例函数?
(3)二次函数?
(4)幂函数?
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知某产品的历史收益率的频率分布直方图如图所示.
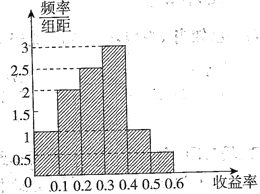
(1)试估计该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
根据表中数据算出![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从表中五组销量数据中随机抽取两组,记其中销量超过6万份的组数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明“1+2+22+…+2n-1=2n-1(n∈N+)”的过程中,第二步n=k时等式成立,则当n=k+1时,应得到( )
A.1+2+22+…+2k-2+2k-1=2k+1-1
B.1+2+22+…+2k+2k+1=2k-1+2k+1
C.1+2+22+…+2k-1+2k+1=2k+1-1
D.1+2+22+…+2k-1+2k=2k+1-1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数 y=f(x) 对任意的x,y∈R,满足条件:f(x+y)=f(x)+f(y)﹣2,且当x>0时,f(x)>2
(1)求f(0)的值;
(2)证明:函数f(x)是R上的单调增函数;
(3)解不等式f(2t2﹣t﹣3)﹣2<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+3在x=2时取得最小值,且函数f(x)的图象在x轴上截得的线段长为2.
(1)求函数f(x)的解析式;
(2)若函数g(x)=f(x)﹣mx的一个零点在区间(0,2)上,另一个零点在区间(2,3)上,求实数m的取值范围.
(3)当x∈[t,t+1]时,函数f(x)的最小值为﹣ ![]() ,求实数t的值.
,求实数t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明“n3+(n+1)3+(n+2)3 , (n∈N+)能被9整除”,要利用归纳法假设证n=k+1时的情况,只需展开( ).
A.(k+3)3
B.(k+2)3
C.(k+1)3
D.(k+1)3+(k+2)3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明“当 n 为正奇数时,xn+yn 能被 x+y 整除”,第二步归纳假
设应该写成( )
A.假设当n=k![]() 时, xk+yk 能被 x+y 整除
时, xk+yk 能被 x+y 整除
B.假设当N=2K ![]() 时, xk+yk 能被 x+y 整除
时, xk+yk 能被 x+y 整除
C.假设当N=2K+1 ![]() 时, xk+yk 能被 x+y 整除
时, xk+yk 能被 x+y 整除
D.假设当 N=2K-1![]() 时, x2k-1+y2k-1 能被 x+y 整除
时, x2k-1+y2k-1 能被 x+y 整除
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com