练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．在平面直角坐标系xOy中，若抛物线y2=2px经过点（4，2），则实数p=$\frac{1}{2}$．

    分析 利用抛物线经过的点，求解即可．

    解答 解：抛物线y2=2px经过点（4，2），
    可得4=8P，
    解得p=$\frac{1}{2}$．
    故答案为：$\frac{1}{2}$．

    点评 本题考查抛物线才的应用，基本知识考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

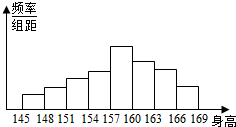    11．为了了解中学生的身高情况，对某中学同龄的若干女生身高进行测量，将所得数据整理后，画出频率分布直方图如图所示，已知图中从左到右五个小组的频率分别为0.017，0.050，0.100，0.133，0.300，第三个小组的频数为6．
    （1）参加这次测试的学生数是多少？
    （2）试问这组身高数据的中位数和众数分别在哪个小组的范围内，且在众数这个小组内人数是多少？
    （3）如果本次测试身高在157cm以上（包括157cm）的为良好，试估计该校女生身高良好率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．长为4的向量$\overrightarrow a$与单位向量$\overrightarrow e$的夹角为$\frac{2π}{3}$，则$\overrightarrow a$在向量$\overrightarrow e$方向上的投影向量为-2$\overrightarrow{e}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知平面向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-2，m），且$\overrightarrow{a}$∥$\overrightarrow{b}$，则|2$\overrightarrow{a}$+3$\overrightarrow{b}$|=（　　）
    A．$2\sqrt{5}$B．$3\sqrt{5}$C．$4\sqrt{5}$D．$5\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知{an}为等差数列，且a3+a4=3（a1+a2），a2n-1=2an．
    （1）求数列{an}的通项公式；
    （2）设数列{bn}的前n项和为Sn，且Sn=m-$\frac{{{a_n}+1}}{2^n}$（m为常数）．令cn=b2n （n∈N*），求数列{cn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．定点P（a，b）在圆x2+y2+2x=1内，直线（a+1）x+by+a-1=0与圆x2+y2+2x=1的位置关系是（　　）
    A．相交B．相离C．相切D．不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．若正实数x，y满足（2xy-1）2=（5y+2）（y-2），则x+$\frac{1}{2y}$的最大值为$\frac{3\sqrt{2}}{2}$-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．点P（1，-1）到直线x-y-4=0的距离是$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．直线$\left\{\begin{array}{l}x={x_0}+at\\ y={y_0}+bt\end{array}\right.$（t为参数）上的两个点A，B对应参数分别为t1，t2，则|AB|=（　　）
    A．|t1-t2|B．$\sqrt{{a^2}+{b^2}}|{{t_1}-{t_2}}|$C．$\frac{{|{{t_1}-{t_2}}|}}{{\sqrt{{a^2}+{b^2}}}}$D．$\frac{{|{{t_1}-{t_2}}|}}{{{a^2}+{b^2}}}$

    查看答案和解析>>

    同步练习册答案